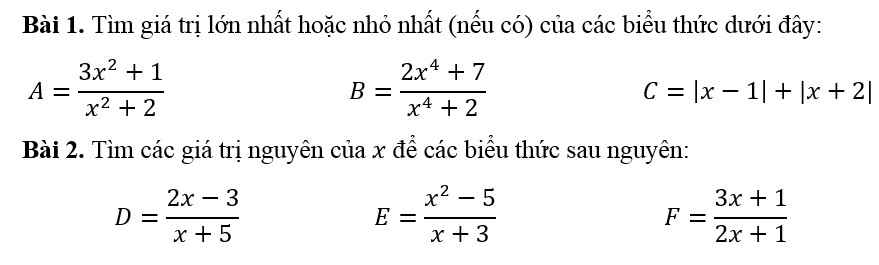Bài 1:
\(A=\dfrac{3\left(x^2+2\right)-5}{x^2+2}=3-\dfrac{5}{x^2+2}\ge3-\dfrac{5}{0+2}=\dfrac{1}{2}\\ A_{min}=\dfrac{1}{2}\Leftrightarrow x=0\\ B=\dfrac{2\left(x^4+2\right)+3}{x^4+2}=2+\dfrac{3}{x^4+2}\le2+\dfrac{3}{0+2}=\dfrac{7}{2}\\ B_{max}=\dfrac{7}{2}\Leftrightarrow x=0\\ C=\left|1-x\right|+\left|x-2\right|\ge\left|1-x+x-2\right|=1\\ C_{min}=1\Leftrightarrow\left(1-x\right)\left(x-2\right)\ge0\Leftrightarrow1\le x\le2\)
Bài 2:
\(D=\dfrac{2\left(x+5\right)-13}{x+5}=2-\dfrac{13}{x+5}\in Z\\ \Leftrightarrow x+5\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\\ \Leftrightarrow x\in\left\{-18;-6;-4;8\right\}\\ E=\dfrac{x\left(x+3\right)-3\left(x+3\right)+4}{x+3}=x-3+\dfrac{4}{x+3}\in Z\\ \Leftrightarrow x+3\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Leftrightarrow x\in\left\{-7;-5;-4;-2;-1;1\right\}\\ 2F=\dfrac{6x+2}{2x+1}=\dfrac{3\left(2x+1\right)-1}{2x+1}=3-\dfrac{1}{2x+1}\\ F\in Z\Leftrightarrow2F\in Z\Leftrightarrow2x+1\inƯ\left(1\right)=\left\{-1;1\right\}\\ \Leftrightarrow x\in\left\{-1;0\right\}\)