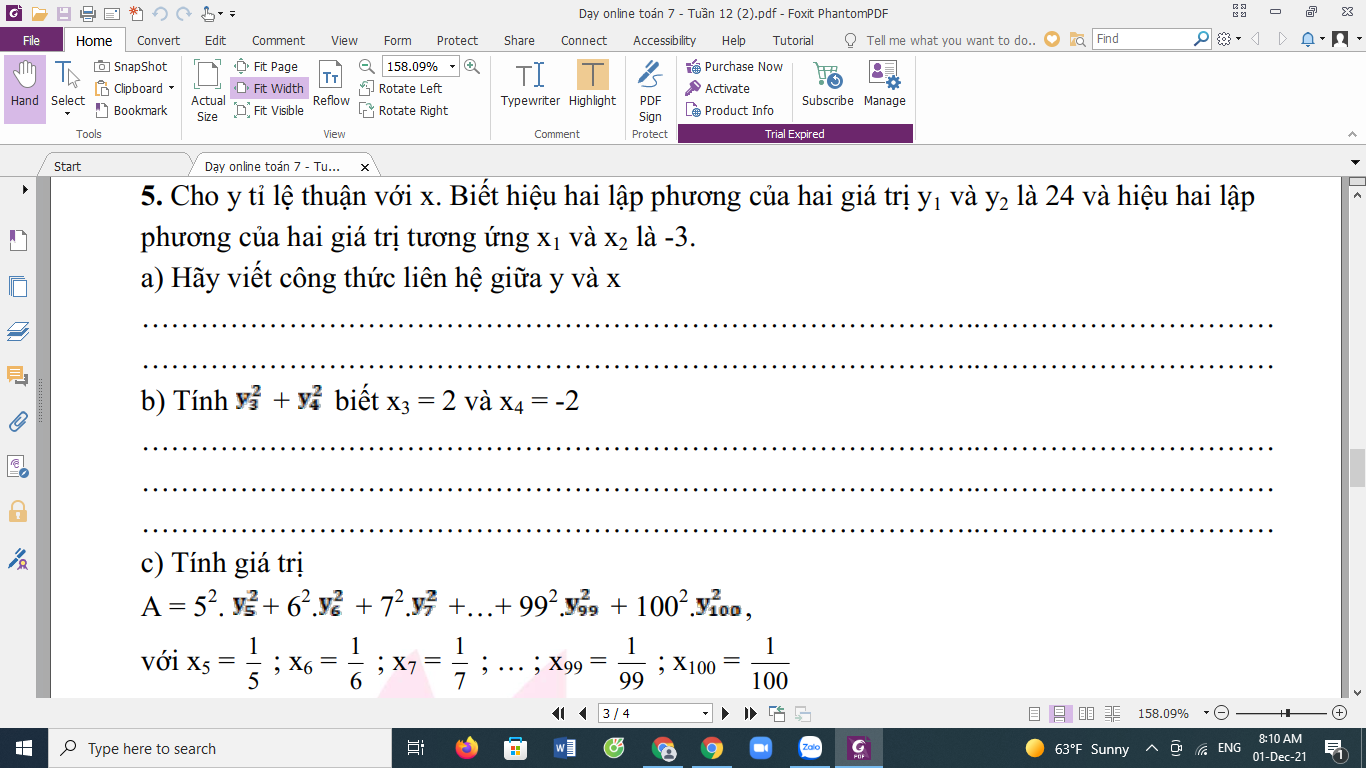
\(a,\) Ta có \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{1}{k}\) (k là hstl)
\(\Rightarrow\dfrac{x_1^3}{y_1^3}=\dfrac{x_2^3}{y_2^3}=\dfrac{x_1^3-x_2^3}{y_1^3-y_2^3}=\dfrac{-3}{24}=-\dfrac{1}{8}\\ \Rightarrow\left\{{}\begin{matrix}x_1^3=-\dfrac{1}{8}y_1^3\\x_2^3=-\dfrac{1}{8}y_2^3\end{matrix}\right.\Rightarrow x^3=-\dfrac{1}{8}y^3\Rightarrow y=-2x\\ c,x_3=2\Rightarrow y_3=-4;x_4=-2\Rightarrow y_4=4\\ \Rightarrow y_3^2+y_4^2=16+16=32\\ c,y_5^2=-2x_5^2=-\dfrac{2}{5^2};y_6^2=-2x_6^2=-\dfrac{2}{6^2}\\ ...\\ y_{100}^2=-2x_{100}^2=-\dfrac{2}{100^2}\\ \Rightarrow A=5^2\cdot\left(-\dfrac{2}{5^2}\right)+6^2\cdot\left(-\dfrac{2}{6^2}\right)+...+100^2\cdot\left(-\dfrac{2}{100^2}\right)\\ \Rightarrow A=-2-2-2-...-2=-2\cdot96=-192\)