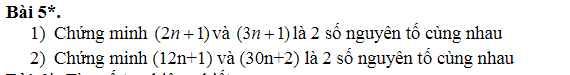1, Gọi d=ƯCLN(2n+1,3n+1)
\(\Rightarrow2n+1⋮d;3n+1⋮d\\ \Rightarrow3n+1-2n-1⋮d\\ \Rightarrow1⋮d\\ \Rightarrow d=1\\ \RightarrowƯCLN\left(2n+1,3n+1\right)=1\)
Vậy ...
2, Gọi d=ƯCLN(12n+1,30n+2)
\(\Rightarrow12n+1⋮d;30n+1⋮d\\ \Rightarrow-2\left(30n+1\right)+5\left(12n+1\right)⋮d\\ \Rightarrow1⋮d\\ \Rightarrow d=1\\ \RightarrowƯCLN\left(2n+1,3n+1\right)=1\)
Vậy ...
2: Vì 12n+1 là số lẻ
và 30n+2 là số chẵn
nên 12n+1 và 30n+2 là hai số nguyên tố cùng nhau
1) -gọi d là ước chung của (2n+1) và (3n+2)
\(\Rightarrow2n+1⋮d\) và \(3n+1⋮d\)
\(\Rightarrow6n+3⋮d\) và \(6n+2⋮d\)
\(\Rightarrow6n+3-6n-2⋮d\)
\(\Rightarrow6n+3-6n-2\)
\(\Rightarrow1⋮d\) \(\Rightarrow d=1\)
Vậy 2n+1 và 3n+1 là hai số nguyên tố