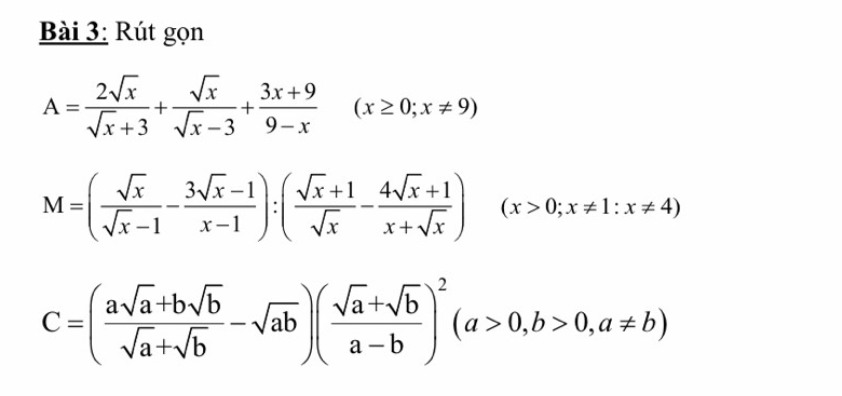\(A=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{-3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{-3}{\sqrt{x}-3}\\ M=\dfrac{x+\sqrt{x}-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\left(\sqrt{x}+1\right)^2-4\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\\ M=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-2\sqrt{x}}\\ M=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
\(C=\left[\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right]\left[\dfrac{\sqrt{a}+\sqrt{b}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\right]^2\\ C=\left(a-\sqrt{ab}+b-\sqrt{ab}\right)\left(\dfrac{1}{\sqrt{a}-\sqrt{b}}\right)^2\\ C=\left(\sqrt{a}-\sqrt{b}\right)^2\cdot\dfrac{1}{\left(\sqrt{a}-\sqrt{b}\right)^2}=1\)
\(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-3}{\sqrt{x}-3}\)
A= \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{3x+9}{9-x}\left(x\ge0;x\ne1;x\ne4\right)\\ =\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{3x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{-3\sqrt{x}—9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{-3}{\sqrt{X}-3}\\ \)
\(M=\left[\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right]:\left[\dfrac{\sqrt{x}+1}{\sqrt{x}}-\dfrac{4\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right]\\ M=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-\left(3\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\left(\sqrt{x}+1\right)^2-\left(4\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\\ M=\dfrac{x+\sqrt{x}-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x+2\sqrt{x}+1-4\sqrt{x}-1}\\ M=\dfrac{x-2\sqrt{x}+1}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}}{x-2\sqrt{x}}=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ M=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)