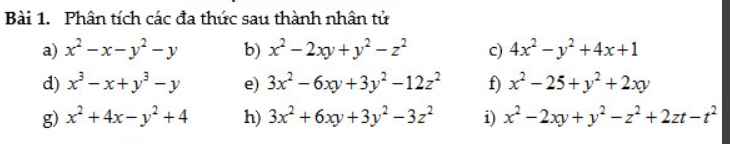\(a,=\left(x-y\right)\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\\ b,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ c,=\left(2x+1\right)^2-y^2=\left(2x+1-y\right)\left(2x+1+y\right)\\ d,=\left(x+y\right)\left(x^2-xy+y^2\right)-\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2-1\right)\\ e,=3\left(x^2-2xy+y^2-4z^2\right)\\ =3\left[\left(x-y\right)^2-4z^2\right]=3\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=\left(x+y\right)^2-25=\left(x+y-5\right)\left(x+y+5\right)\\ g,=\left(x+2\right)^2-y^2=\left(x+y-2\right)\left(x-y+2\right)\\ h,=3\left(x^2+2xy+y^2-z^2\right)=3\left[\left(x+y\right)^2-z^2\right]\\ =3\left(x+y-z\right)\left(x+y+z\right)\\ i,=\left(x-y\right)^2-\left(z-t\right)^2=\left(x-y-z+t\right)\left(x-y+z-t\right)\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC cân tại A.Trên tia đối của tia BC lấy điểm M trên tia đối của tia CB lấy điểm N sao cho BM=CN.
a) Chứng minh rằng tam giác AMN là tam giác cân.
b) Kẻ BH vuông tại AM,kẻ CK vuông AN.Chứng minh rằng BH=CK;AH=AK.
c) Gọi O là giao điểm của HB và KC.Tam giác OBC là tam giác gì? Chứng minh BC=HK
Bài 1: Thu gọn các đơn thức sau rồi cho biết phần hệ số, phần biến của mỗi đơn thức:a, b, c, d, e,
Đọc tiếp
Bài 1: Thu gọn các đơn thức sau rồi cho biết phần hệ số, phần biến của mỗi đơn thức:
a, b,
c,
d, e,
CHO A= 8a-2b + 4a-b với a-b=9 a và b khác 3
3a+9 3b-a
AI TÍNH GIÚP MÌNH VỚI Ạ
CẢM ƠN NHIỀU
Điểm kiểm tra môn toán của lớp 7A được thống kê như sau7 10 5 7 8 10 6 5 7 87 6 4 10 3 4 8 9 9 94 7 3 9 2 3 7 5 9 7 5 7 6 4 9 5 8 5 6 3a) Dấu hiệu ở đây là gì? Số các giá trị? Số các giá trị khác nhau là bao nhiêu?b) Lập bảng tần số?c) Hãy tính số trung bình cộng và tìm mốt của dấu hiệu?d) Vẽ bểu đồ đoạn thẳng, nhận xét về việc học toán của học sinh lớp 7A?
Đọc tiếp
Điểm kiểm tra môn toán của lớp 7A được thống kê như sau
7 10 5 7 8 10 6 5 7 8
7 6 4 10 3 4 8 9 9 9
4 7 3 9 2 3 7 5 9 7
5 7 6 4 9 5 8 5 6 3
a) Dấu hiệu ở đây là gì? Số các giá trị? Số các giá trị khác nhau là bao nhiêu?
b) Lập bảng '' tần số''?
c) Hãy tính số trung bình cộng và tìm mốt của dấu hiệu?
d) Vẽ bểu đồ đoạn thẳng, nhận xét về việc học toán của học sinh lớp 7A?
Tính giá trị của các biểu thức sau biết x+y+1=0
N=x^2(x+y)-y^2(x+y)+x^2-y^2+2(x+y)+3
Cho tam giác cân ở A có AB=AC=17cm,BC=16cm. Kẻ trung tuyến AM. Cm rằng:
a, AM (vuông góc) BC
b, Tính độ dài AM
Cho tam giác ABC, M và N lần lượt là trung điểm của các cạnh AB và AC. Từ B kẻ đường phân giác trong và phân giác ngoài của tam giác ABC và cắt đường thẳng MN lần lượt tại H và K. Các tia AH và AK cắt đường thẳng BC thứ tự tại P và Q. Chứng minh rằng: a,BH vuông góc với AP b,B là trung điểm của PQ ...
Đọc tiếp
Cho tam giác ABC, M và N lần lượt là trung điểm của các cạnh AB và AC. Từ B kẻ đường phân giác trong và phân giác ngoài của tam giác ABC và cắt đường thẳng MN lần lượt tại H và K. Các tia AH và AK cắt đường thẳng BC thứ tự tại P và Q. Chứng minh rằng: a,BH vuông góc với AP b,B là trung điểm của PQ c,AB=HK?
Không cần vẽ hinh chỉ cần ghi lời giải thôi mình đang cần gấp
cho các số x,y,ztir lệ với các số 5;4;3. tính giá trị của P=x+2y-3z/x-2y+3z
cho tam giác MNP vuông tại M N bé hơn MP tia phân giác của MNP cắt MP tại K và k vectơ AE vuông góc với NP Chứng minh tam giác MNK bằng tam giác akd tia de cắt tia nm tại f chứng minh n s = n p Gọi I là trung điểm của FP chứng minh n k i thẳng hàng
Xem chi tiết
cho tam giác ABC có điểm D nằm trong tam giác và AD=AB.tia BD cắt đoạn AC ở I . H là trung điểm của BD a) chứng minh AH vuông góc với BD b)So sánh AD và AI c) chứng minh AB