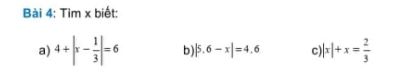Question

Answer 1

a) \(4+\left|x-\dfrac{1}{3}\right|=6\)

 \(\Rightarrow\left|x-\dfrac{1}{3}\right|=2\)

\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=2\\x-\dfrac{1}{3}=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)

b) \(\left|5,6-x\right|=4,6\)

\(\Rightarrow\left[{}\begin{matrix}5,6-x=4,6\\5,6-x=-4,6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=1\\x=10,2\end{matrix}\right.\)

c) \(\left|x\right|+x=\dfrac{2}{3}\left(đk:x\le\dfrac{2}{3}\right)\)

\(\Rightarrow\left|x\right|=\dfrac{2}{3}-x\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}-x\left(\dfrac{2}{3}\ge x\ge0\right)\\x=x-\dfrac{2}{3}\left(x< 0\right)\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\left(tm\right)\\0=-\dfrac{2}{3}\left(VLý\right)\end{matrix}\right.\)

Answer 2

a. x=7/3 hoặc x= -5/3

b. x=1 hoặc x= 10,2

c. x=1/3 

 

Answer 3

a, \(4+\left|x-\dfrac{1}{3}\right|=6 \)
\(\left|x-\dfrac{1}{3}\right|=6-4=2\)
\(\cdot x-\dfrac{1}{3}=2\)
x= 2\(\dfrac{1}{3}\)
\(\cdot x-\dfrac{1}{3}=-2\)
x=\(-\dfrac{5}{3}\)
Vậy x\(\left\{2\dfrac{1}{3};-\dfrac{5}{3}\right\}\)
b,\(\left|5.6-x\right|=4.6\)
\(\left|5.6-x\right|=24 \)
* 5.6-x= 24
x= 6
* 5.6-x= -24
x= 54
Vậy x{ 6; 54}