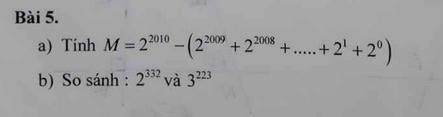a)
+ Đặt N= \(2^{2009}+2^{2008}+...+2^1+2^0\)
\(\Rightarrow2N=2^{2010}+2^{2009}+...+2^1\)
\(\Rightarrow N=2N-N=2^{2010}+2^{2009}+...+2^1-2^{2009}-2^{2008}-...-2^0=2^{2010}-2^0=2^{2010}-1\)
\(\Rightarrow M=2^{2010}-2^{2010}+1=1\)
b) \(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Do \(8^{111}< 9^{111}\Rightarrow2^{332}< 3^{223}\)
có \(2^{332}< 2^{333}\)
\(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
mà \(8^{111}< 9^{111}\)
=>\(2^{332}< 2^{333}< 3^{222}< 3^{223}\)