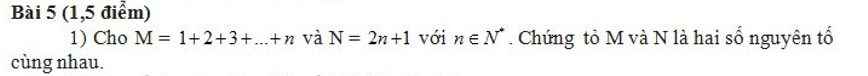Question

Answer 1

Lời giải:

$M=\frac{n(n+1)}{2}$

$N=2n+1$

Giả sử $M,N$ không nguyên tố cùng nhau. Gọi $p$ là ước nguyên tố lớn nhất của $M,N$

$\frac{n(n+1)}{2}\vdots p\Rightarrow n(n+1)\vdots p$

$\Rightarrow n\vdots p$ hoặc $n+1\vdots p$

Nếu $n\vdots p$. Kết hợp $2n+1=n+n+1\vdots p$

$\Rightarrow 1\vdots p\Rightarrow p=1$ (vô  lý)

Nếu $n+1\vdots p$. Kết hợp $2n+1=n+n+1\vdots p$

$\Rightarrow n\vdots p$

$\Rightarrow 1=(n+1)-n\vdots p\Rightarrow p=1$ (vô lý)

Vậy điều giả sử là sai, có nghĩa là $M,N$ nguyên tố cùng nhau.