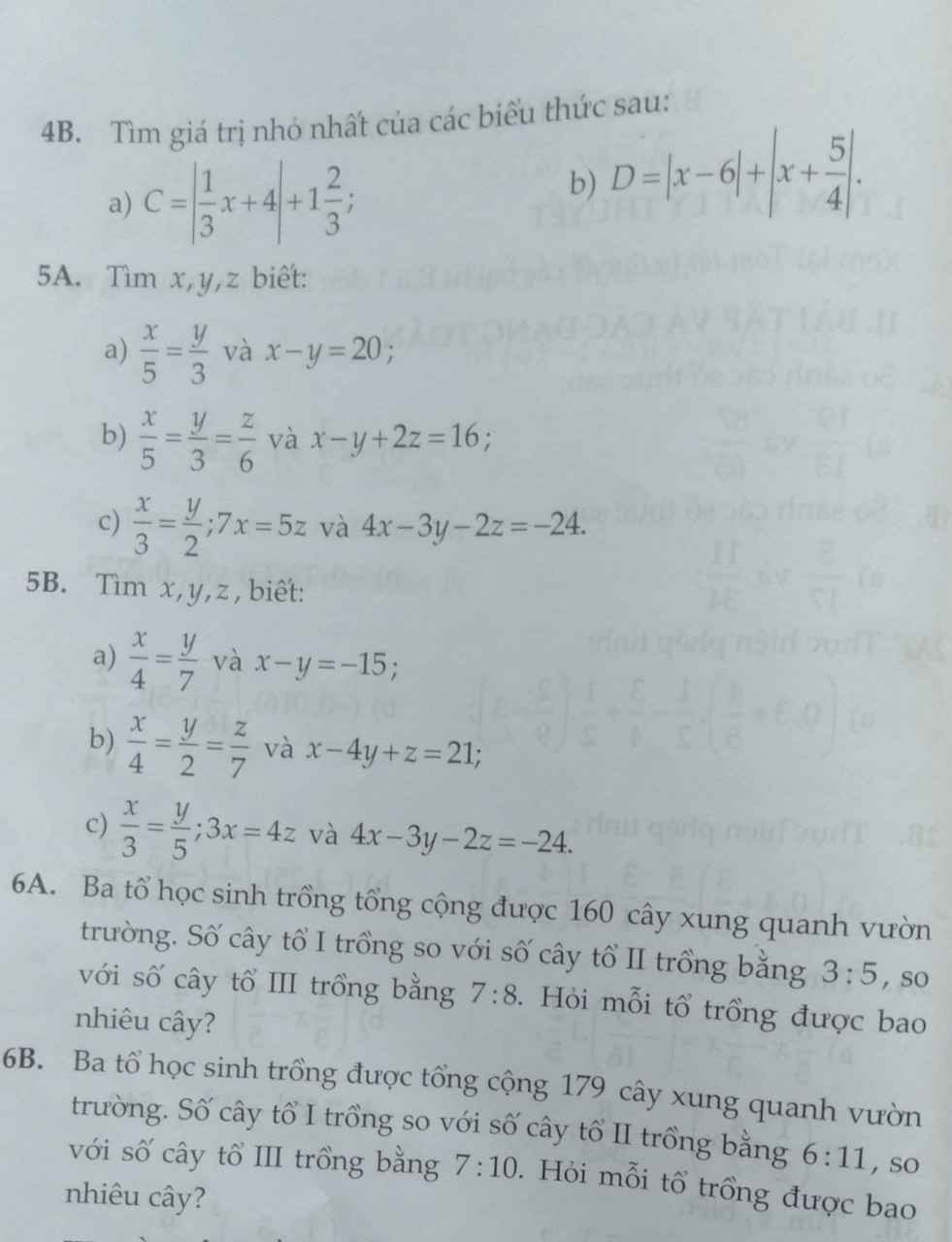Bài 4A:
a: Ta có: \(\left|x-\dfrac{7}{4}\right|\ge0\forall x\)
\(\Leftrightarrow\left|x-\dfrac{7}{4}\right|+\dfrac{8}{5}\ge\dfrac{8}{5}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{7}{4}\)
Bài 6A:
Gọi số cây tổ 1, tổ 2 và tổ 3 trồng được lần lượt là a,b,c
Theo đề, ta có: \(\left\{{}\begin{matrix}\dfrac{a}{b}=\dfrac{3}{5}\\\dfrac{a}{c}=\dfrac{7}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{3}=\dfrac{b}{5}\\\dfrac{a}{7}=\dfrac{c}{8}\end{matrix}\right.\Leftrightarrow\dfrac{a}{21}=\dfrac{b}{35}=\dfrac{c}{24}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{21}=\dfrac{b}{35}=\dfrac{c}{24}=\dfrac{a+b+c}{21+35+24}=\dfrac{160}{80}=2\)
Do đó: a=42; b=70; c=48
Bài 6B:
Gọi số cây tổ 1, tổ 2 và tổ 3 trồng được lần lượt là a,b,c
Theo đề, ta có: \(\left\{{}\begin{matrix}\dfrac{a}{b}=\dfrac{6}{11}\\\dfrac{a}{c}=\dfrac{7}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{6}=\dfrac{b}{11}\\\dfrac{a}{7}=\dfrac{c}{10}\end{matrix}\right.\Leftrightarrow\dfrac{a}{42}=\dfrac{b}{77}=\dfrac{c}{60}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{42}=\dfrac{b}{77}=\dfrac{c}{60}=\dfrac{a+b+c}{42+77+60}=\dfrac{179}{179}=1\)
Do đó: a=42; b=77; c=60