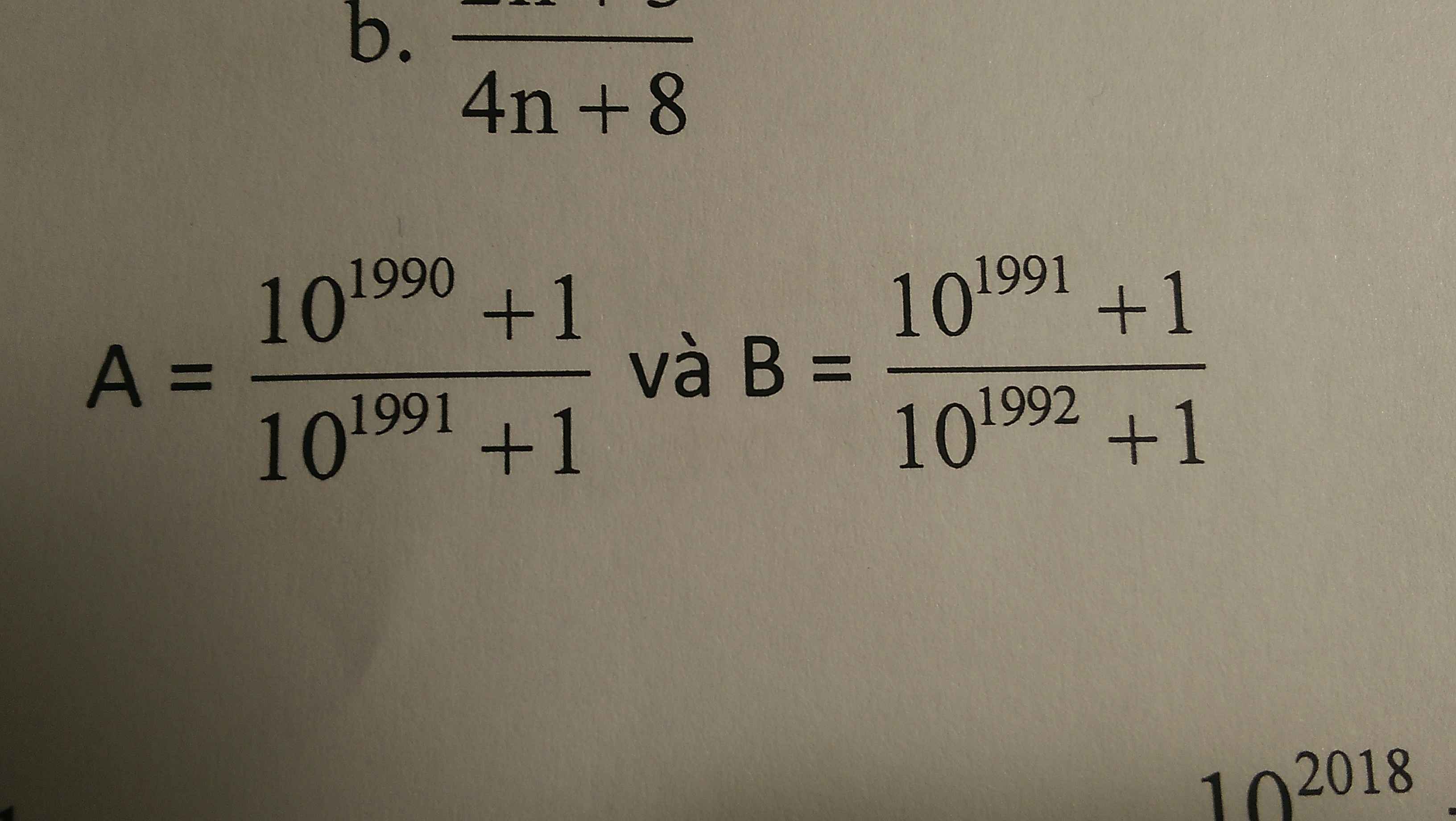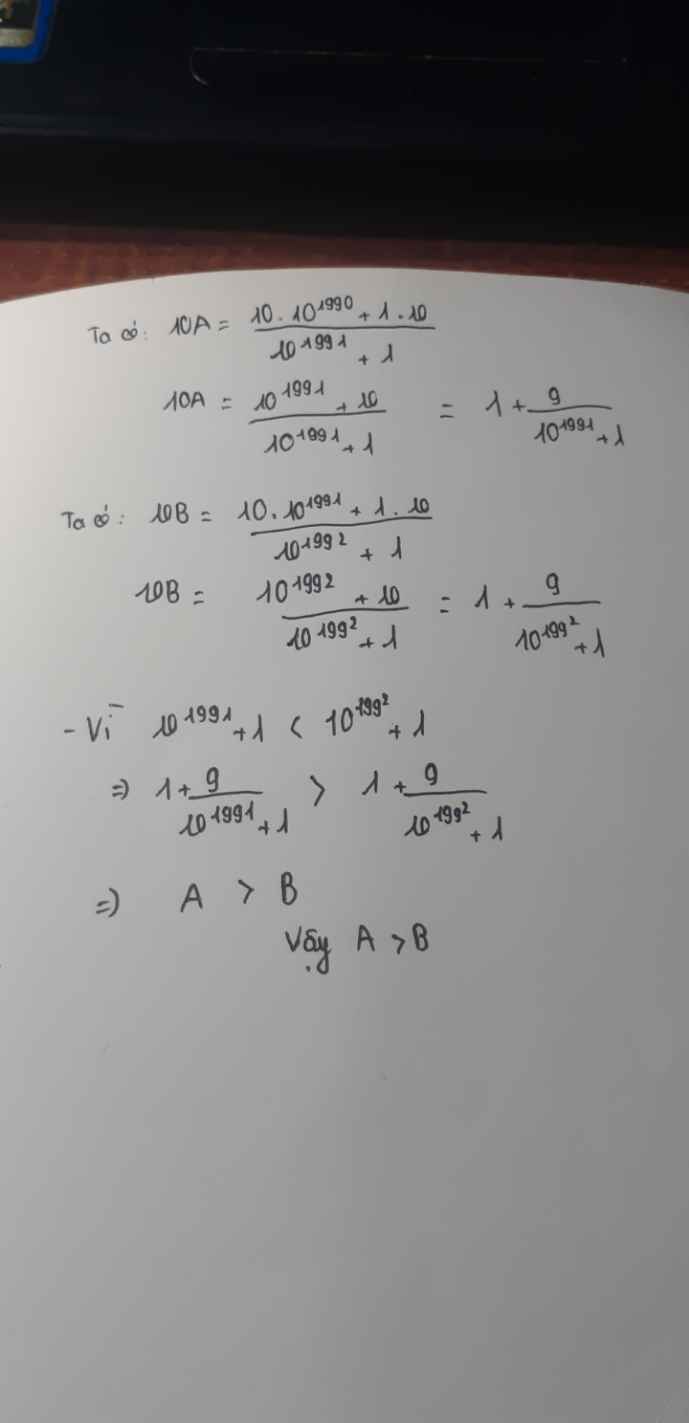Ta có: \(10A=\dfrac{10^{1991}+10}{10^{1991}+1}=1+\dfrac{9}{10^{1991}+1}\)
\(10B=\dfrac{10^{1992}+10}{10^{1992}+1}=1+\dfrac{9}{10^{1992}+1}\)
Ta có: \(10^{1991}+1< 10^{1992}+1\)
nên \(\dfrac{9}{10^{1991}+1}>\dfrac{9}{10^{1992}+1}\)
\(\Leftrightarrow10A>10B\)
hay A>B
Giải:
\(A=\dfrac{10^{1990}+1}{10^{1991}+1}\) và \(B=\dfrac{10^{1991}+1}{10^{1992}+1}\)
Ta có:
\(A=\dfrac{10^{1990}+1}{10^{1991}+1}\)
\(10A=\dfrac{10^{1991}+10}{10^{1991}+1}\)
\(10A=\dfrac{10^{1991}+1+9}{10^{1991}+1}\)
\(10A=1+\dfrac{9}{10^{1991}+1}\)
Tương tự :
\(B=\dfrac{10^{1991}+1}{10^{1992}+1}\)
\(10B=\dfrac{10^{1992}+10}{10^{1992}+1}\)
\(10B=\dfrac{10^{1992}+1+9}{10^{1992}+1}\)
\(10B=1+\dfrac{9}{10^{1992}+1}\)
Vì \(\dfrac{9}{10^{1991}+1}>\dfrac{9}{10^{1992}+1}\) nên \(10A>10B\)
\(\Rightarrow A>B\)