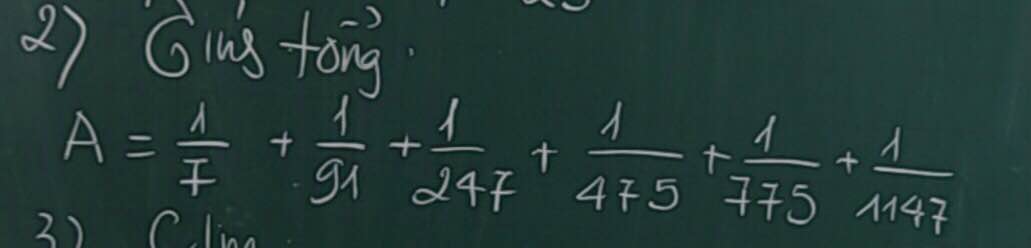Giải:
\(A=\dfrac{1}{7}+\dfrac{1}{91}+\dfrac{1}{247}+\dfrac{1}{475}+\dfrac{1}{775}+\dfrac{1}{1147}\)
\(A=\dfrac{1}{1.7}+\dfrac{1}{7.13}+\dfrac{1}{13.19}+\dfrac{1}{19.25}+\dfrac{1}{25.31}+\dfrac{1}{31.37}\)
\(A=\dfrac{1}{6}.\left(\dfrac{6}{1.7}+\dfrac{6}{7.13}+\dfrac{6}{13.19}+\dfrac{6}{19.25}+\dfrac{6}{25.31}+\dfrac{6}{31.37}\right)\)
\(A=\dfrac{1}{6}.\left(1-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{25}+\dfrac{1}{25}-\dfrac{1}{31}+\dfrac{1}{31}-\dfrac{1}{37}\right)\)
\(A=\dfrac{1}{6}.\left(1-\dfrac{1}{37}\right)\)
\(A=\dfrac{1}{6}.\dfrac{36}{37}\)
\(A=\dfrac{6}{37}\)
\(6A=\dfrac{6}{1.7}+\dfrac{6}{7.13}+\dfrac{6}{13.19}+...+\dfrac{6}{31.37}\)
= \(1-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{19}+...+\dfrac{1}{31}-\dfrac{1}{37}=\dfrac{36}{37}\)
<=> A = \(\dfrac{6}{37}\)
Ta có: \(A=\dfrac{1}{7}+\dfrac{1}{91}+\dfrac{1}{247}+\dfrac{1}{475}+\dfrac{1}{775}+\dfrac{1}{1147}\)
\(=\dfrac{1}{6}\left(\dfrac{6}{1\cdot7}+\dfrac{6}{7\cdot13}+\dfrac{6}{13\cdot19}+\dfrac{6}{19\cdot25}+\dfrac{6}{25\cdot31}+\dfrac{6}{31\cdot37}\right)\)
\(=\dfrac{1}{6}\left(1-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{25}+\dfrac{1}{25}-\dfrac{1}{31}+\dfrac{1}{31}-\dfrac{1}{37}\right)\)
\(=\dfrac{1}{6}\left(1-\dfrac{1}{37}\right)\)
\(=\dfrac{1}{6}\cdot\dfrac{36}{37}=\dfrac{6}{37}\)