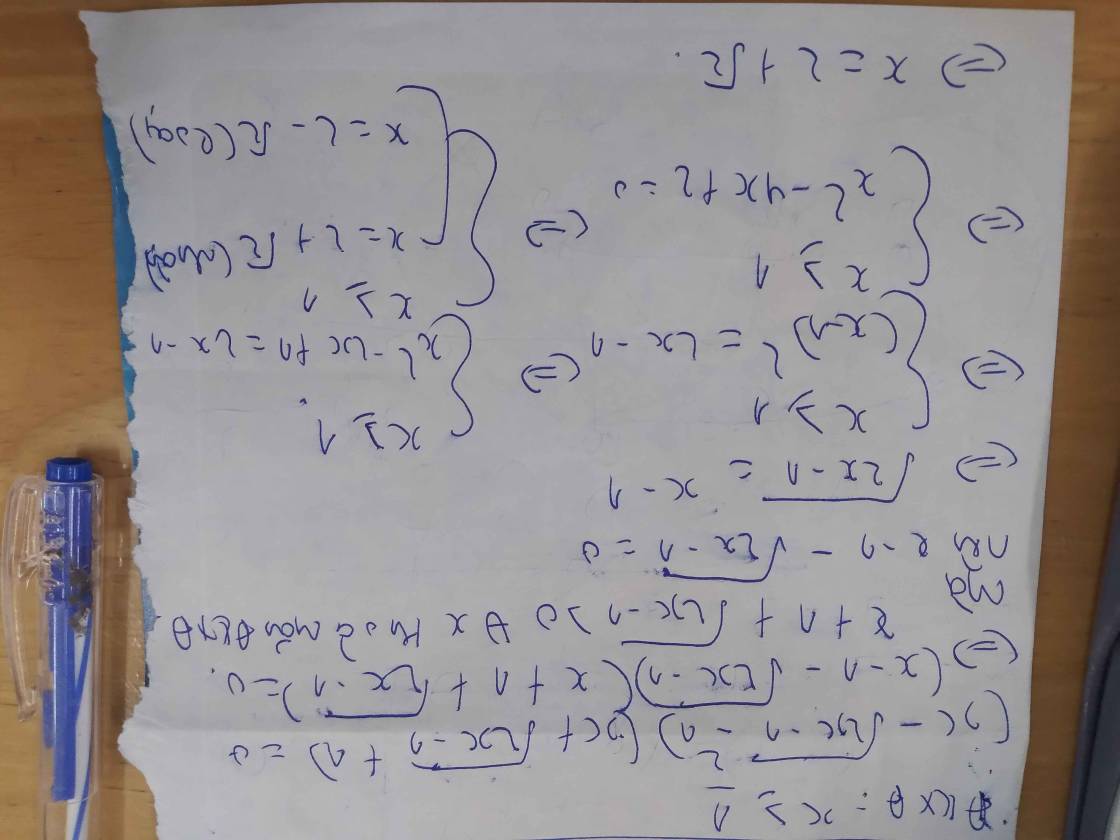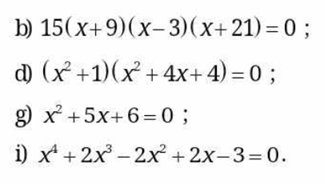( x - √2x - 1 -1)( x + √2x -1 + 1) = 0
Bài 4: Phương trình tích
Giải các phương trình bậc hai sau bằng cách đưa về dạng phương trình tích:
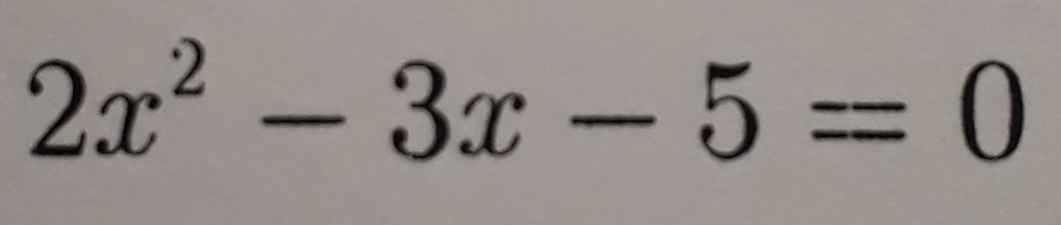
\(2x^2-3x-5=0 \\ \Leftrightarrow2x^2+2x-5x-5=0\\ \Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\\ \Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5\\x=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\\ Vậy.S=\left\{\dfrac{5}{2};-1\right\}\)
Đúng 2
Bình luận (0)
\(2x^2-3x-5=0\)
\(\Leftrightarrow2x^2+2x-5x-5=0\)
\(\Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\)
Vậy \(x=\dfrac{5}{2};x=-1\) là các nghiệm của phương trình.
#\(Toru\)
Đúng 1
Bình luận (0)
b: =>(x+9)(x-3)(x+21)=0
=>x+9=0; x-3=0; x+21=0
=>x=-9; x=3;x=-21
g: =>(x+2)(x+3)=0
=>x=-2 hoặc x=-3
d: =>x^2+4x+4=0
=>(x+2)^2=0
=>x+2=0
=>x=-2
Đúng 0
Bình luận (0)
giải pt
0=(x-2)^2(x+2)
\(0=\left(x-2\right)^2\left(x+2\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-2\right)^2=0\\x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Trong các pt sau, pt tích là
A.(x-2)^2(x+2)=2
B.0=(x-2)^2(x+2)
C.(x-2)^2(x+2)=2(x+2)
D. (x-2)^2(x+2)+(x+2)
Trong các pt sau, pt tích là
A.(x-2)^2(x+2)=2
B.0=(x-2)^2(x+2)
C.(x-2)^2(x+2)=2(x+2)
D. (x-2)^2(x+2)+(x+2)
Đúng 0
Bình luận (1)
B. 0 = (x - 2)²(x + 2)
C. (x - 2)²(x + 2) = 2(x + 2)
Đúng 0
Bình luận (0)
2x^2+8x-10=0
\(2x^2+8x-10=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Phương trình nào sau đây là ptrinh tích ?
A.2x-(x+3)
B.2x+3=0
C.14x+7=0
D.(x-5)(x-3)=0
Giải pt sau:
2(x2 - x) - x(x + 2) + 4 = 0
Giúp mik vs mọi người ơi
\(2\left(x^2-x\right)-x\left(x+2\right)+4=0\)
\(\Leftrightarrow2x^2-2x-x^2-2x+4=0\)
\(\Leftrightarrow x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)
Vậy \(S=\left\{2\right\}\)
Đúng 2
Bình luận (0)
Giải phương trình sau:
(x2 - 2) - (x - 2)(3x - 7) = 0
\(\left(x^2-2\right)-\left(x-2\right)\left(3x-7\right)=0\\ \Leftrightarrow x^2-2-\left(3x^2-6x-7x+14\right)=0\\ \Leftrightarrow x^2-2-3x^2+13x-14=0\\ \Leftrightarrow-2x^2+13x-16=0\\\Leftrightarrow \left[{}\begin{matrix}x=\dfrac{13+\sqrt{41}}{4}\\x=\dfrac{13-\sqrt{41}}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
19x-7=0
\(19x-7=0\)
\(\Leftrightarrow19x=7\)
\(\Leftrightarrow x=\dfrac{7}{19}\)
Đúng 0
Bình luận (0)