1. Tính nhẩm nghiệm của các phương trình :
a/ 5x ^ 2 - 32x + 27 = 0
b/ 2x ^ 2 + (1 + sqrt(2)) * x - (3 + sqrt(2)) = 0
c/ 6x ^ 2 - 75x - 81 = 0
d/ 3x ^ 2 + (3 - sqrt(2)) * x - sqrt(2) = 0
e/ x ^ 2 - (sqrt(3) + sqrt(5)) * x + sqrt(15) = 0
f/ x ^ 2 - (2 + sqrt(3)) * x + 2sqrt(3) = 0
\(a.x_1=5,4;x_2=1\\ b.x=\dfrac{-\left(1+\sqrt{2}\right)\pm\sqrt{27+10\sqrt{2}}}{4}\\ c.x_1=13,5;x_2=-1\\ d.x=\dfrac{-3+\sqrt{2}\pm\sqrt{11+6\sqrt{2}}}{6}\\ e.x=\dfrac{\sqrt{3}+\sqrt{5}\pm\sqrt{8-2\sqrt{15}}}{2}\\ f.x=\dfrac{2+\sqrt{3}\pm\sqrt{7-4\sqrt{3}}}{2}\)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O hai đường kính AB và CD vuông góc với nhau. qua điểm M thuộc cung AC nhỏ( M khác A, M khác C). kẻ tiếp tuyến với đường tròn cắt AB, CD lần lượt tại E và F. CM góc MFO= 2 lần góc MBO
( help me, vẽ hình và giải hộ me:( )
Cho đường tròn tâm O hai đường kính AB và CD vuông góc với nhau. qua điểm M thuộc cung AC nhỏ( M khác A, M khác C). kẻ tiếp tuyến với đường tròn cắt AB, CD lần lượt tại E và F. CM góc MFO= 2 lần góc MBO
( help me, vẽ hình và giải hộ me:( )
Cho đường tròn tâm O hai đường kính AB và CD vuông góc với nhau. qua điểm M thuộc cung AC nhỏ( M khác A, M khác C). kẻ tiếp tuyến với đường tròn cắt AB, CD lần lượt tại E và F. CM góc MFO= 2 lần góc MBO
Cho hệ phương trình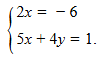
a) Hệ phương trình trên có là một hệ hai phương trình bậc nhất hai ẩn không? Vì sao?
b) Cặp số (–3; 4) có là một nghiệm của hệ phương trình đã cho hay không? Vì sao?
a. phải vì có hai ẩn (x; y) đều là mũ 1
b. \(\left\{{}\begin{matrix}2x=-6\\5x+4y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+0y=-6\\5x+4y=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-3\\y=4\end{matrix}\right.\)
vậy cặp số (-3; 4) là nghiệm của hệ phương trình đã cho
Đúng 1
Bình luận (0)
Bài 4(TT): Cho parabol (P) y x ^ 2 và đường thẳng (d) y 6x - 2m + 3 Gọi x1, x2 là các hoành độ giao điểm của (P) và (d). Tìm m sao cho (x_{1} ^ 2 - 5x_{1} + 2m - 4)(x_{2} ^ 2 - 5x_{2} + 2m - 4) 2 giúp gấp với ạ
Đọc tiếp
Bài 4(TT): Cho parabol (P) y = x ^ 2 và đường thẳng (d) y = 6x - 2m + 3 Gọi x1, x2 là các hoành độ giao điểm của (P) và (d). Tìm m sao cho (x_{1} ^ 2 - 5x_{1} + 2m - 4)(x_{2} ^ 2 - 5x_{2} + 2m - 4) = 2  giúp gấp với ạ
giúp gấp với ạ
Cho phương trình x2 - 2(k-1)x-4k=0
Tìm k để phương trình có hai nghiệm phân biệt x1x2 thỏa mãn 3x1-x2=2
Để phương trình có hai nghiệm phân biệt:
\(\Delta'>0\)
\(\Leftrightarrow\left[-\left(k-1\right)\right]^2+4k>0\)
\(\Leftrightarrow k^2-2k+1+4k>0\)
\(\Leftrightarrow k^2+2k+1>0\)
\(\Leftrightarrow k\ne-1\)
Theo định lý viet:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(k-1\right)\\x_1.x_2=-4k\left(1\right)\end{matrix}\right.\)
Ta có \(\left\{{}\begin{matrix}x_1+x_2=2k-2\\3x_1-x_2=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x_1=2k\\x_1+x_2=2k-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{k}{2}\\\dfrac{k}{2}+x_2=2k-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{k}{2}\\x_2=\dfrac{3k}{2}-2\end{matrix}\right.\)
\(x_1.x_2=-4k\)
\(\Leftrightarrow\dfrac{k}{2}.\left(\dfrac{3k}{2}-2\right)=-4k\)
\(\Leftrightarrow\dfrac{3k^2}{4}-k=-4k\)
\(\Leftrightarrow\dfrac{3k^2}{4}+3k=0\Leftrightarrow3k\left(\dfrac{k}{4}+1\right)=0\)
Tới đây e tính được k=0 hoặc k = -4
Đúng 1
Bình luận (0)
c) Cho phương trình: x2x2-7x+q0, biết hiệu 2 nghiệm bằng 11. Tìm q và hai nghiệm của phương trình d) Tìm q và hai nghiệm của phương trình: x2x2-qx+500 ,biết phương trình có hai nghiệm và có một nghiệm bằng 2 lần nghiệm kia.
Đọc tiếp
c) Cho phương trình: x-7x+q=0, biết hiệu 2 nghiệm bằng 11. Tìm q và hai nghiệm của phương trình
d) Tìm q và hai nghiệm của phương trình:-qx+50=0 ,biết phương trình có hai nghiệm và có một nghiệm bằng 2 lần nghiệm kia.
\(p=\dfrac{a}{a^2+3}+\dfrac{b}{b^2+3}+\dfrac{c}{c^2+3}\)
tìm min p =? với a,b,c thuộc N











