cho tam giác ABC vuông tại A, có đường cao AH.
a) Trên cạnh AC lấy điểm D ( D khác A và C ). Kẻ AI vuông BD tại I. Chứng minh: BH.BC=BI.BD
c) Chứng minh sin góc ADB.sin góc ACB= HI:CD
a: ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(1\right)\)
Xét ΔADB vuông tại A có AI là đường cao
nên \(BI\cdot BD=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=BI\cdot BD\)
b:
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
Xét ΔABD vuông tại A có \(sinADB=\dfrac{AB}{BD}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH=\dfrac{BA^2}{BC}\)
\(BI\cdot BD=BH\cdot BC\)
=>\(\dfrac{BI}{BC}=\dfrac{BH}{BD}\)
Xét ΔBIH và ΔBCD có
\(\widehat{IBH}\) chung
\(\dfrac{BI}{BC}=\dfrac{BH}{BD}\)
Do đó: ΔBIH đồng dạng với ΔBCD
=>\(\dfrac{BH}{BD}=\dfrac{HI}{CD}\)
\(sinADB\cdot sinACB\)
\(=\dfrac{AB}{BD}\cdot\dfrac{AB}{BC}\)
\(=\dfrac{AB^2}{BD\cdot BC}=\dfrac{BH}{BD}\)
\(=\dfrac{HI}{CD}\)
Cho tam giác ABC cân tại A, có đường cao AH = 32 cm, đường cao BK = 38,4 cm.
a) tính các cạnh của tam giác ABC. b) đường trung trực của AC cắt AH tại O, tính OH GIÚP MÌNH VS Ạ
Cho tam giác MNP vương tại M, viết các tí số lượng giác của góc N?
Xét ΔMNP vuông tại M có
\(sinN=\dfrac{MP}{NP}\)
\(cosN=\dfrac{MN}{NP}\)
\(tanN=\dfrac{MP}{MN}\)
\(cotN=\dfrac{NM}{MP}\)
Cho tam giác ABC vuông tại A đường cao AH AH=9cm AC=16cm a) tính các góc còn lại trong tam giác b)viết tỉ số lượng giác của góc B c) tính góc C
a,c: ΔAHC vuông tại H
=>\(AH^2+HC^2=AC^2\)
=>\(HC=\sqrt{16^2-9^2}=5\sqrt{7}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AC^2=CH\cdot CB\)
=>\(CB=\dfrac{16^2}{5\sqrt{7}}=\dfrac{256}{5\sqrt{7}}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(sinB=\dfrac{AC}{BC}=16:\dfrac{256}{5\sqrt{7}}=\dfrac{5\sqrt{7}}{16}\)
=>\(\widehat{B}\simeq56^0\)
=>\(\widehat{C}=90^0-56^0=34^0\)
b: \(sinB=\dfrac{5\sqrt{7}}{16}\)
=>\(cosB=\sqrt{1-sin^2B}=\dfrac{9}{16}\)
\(tanB=\dfrac{5\sqrt{7}}{16}:\dfrac{9}{16}=\dfrac{5\sqrt{7}}{9}\)
\(cotB=1:\dfrac{5\sqrt{7}}{9}=\dfrac{9}{5\sqrt{7}}\)
\(sinC=\dfrac{AH}{AC}=\dfrac{9}{16}\)
\(\Rightarrow\widehat{C}\simeq34,2\)
\(\Rightarrow\widehat{B}=180^o-90^o-34,2^o=55,8^o\)
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}\\cosB=\dfrac{AB}{BC}\\tanB=\dfrac{AC}{AB}\\cotB=\dfrac{AB}{AC}\end{matrix}\right.\)
Trục căn thức ở mẫu a) Căn5/căn7 b)2/căn a-1(với a>_ 0 và a khác 1)
a: \(\dfrac{\sqrt{5}}{\sqrt{7}}=\dfrac{\sqrt{5\cdot7}}{7}=\dfrac{\sqrt{35}}{7}\)
b: \(\dfrac{2}{\sqrt{a}-1}=\dfrac{2\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}=\dfrac{2\sqrt{a}+2}{a-1}\)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC. a) Viết tỉ số lượng giác góc B của AABC. b) Cho AB=6cm, AC = 8cm . Tính BC,AH c ) Chứng minh: AE.AB = AF AC
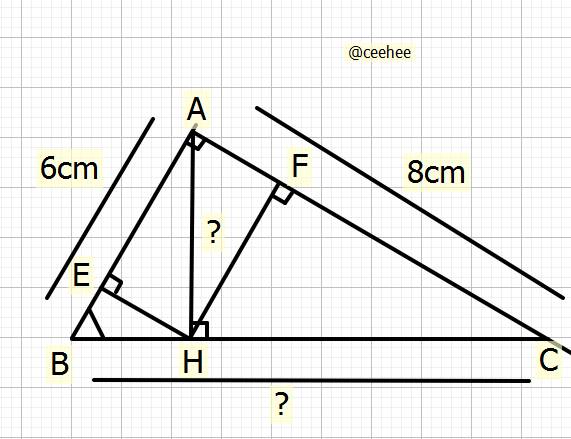
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)
một cái thang dài 5m dựa vào tường tạo với mặt đất một góc 60 độ hỏi chân thang cách tường bao nhiêu mét
Gọi độ dài cái thang là BC, khoảng cách từ chân thang đến chân tường là AB
Theo đề, ta có: BC=5m; AB\(\perp\)AC tại A; \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}\)
=>\(\dfrac{BA}{5}=cos60=\dfrac{1}{2}\)
=>\(BA=\dfrac{5}{2}=2,5\left(m\right)\)
Vậy: Khoảng cách từ chân thang đến chân tường là 2,5m
a) Tìm điều kiện để các căn thức sau có nghĩa: căn x-10 b) đưa thừa số ra ngoài dấu căn: a cân9²b(a>_0) c) so sánh: 2căn3+1 và 2căn2+căn5
a: ĐKXĐ: x-10>=0
=>x>=10
b: \(\sqrt{9a^2b}=\sqrt{\left(3a\right)^2\cdot b}=3a\cdot\sqrt{b}\)
c: \(\left(2\sqrt{3}+1\right)^2=13+4\sqrt{3}\)
\(\left(2\sqrt{2}+\sqrt{5}\right)^2=8+5+2\cdot2\sqrt{2}\cdot\sqrt{5}=13+4\sqrt{10}\)
mà \(4\sqrt{3}< 4\sqrt{10}\left(3< 10\right)\)
nên \(\left(2\sqrt{3}+1\right)^2< \left(2\sqrt{2}+\sqrt{5}\right)^2\)
=>\(2\sqrt{3}+1< 2\sqrt{2}+\sqrt{5}\)
Cho tam giác ABC vuông tại A, góc C=30°, BC=12cm, giải tam giác ABC.
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}+30^0=90^0\)
=>\(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{12}=sin30=\dfrac{1}{2}\)
=>AB=6(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=144-36=108\)
=>\(AC=6\sqrt{3}\left(cm\right)\)
ABC vuông tại A
⇒ ∠B + ∠C = 90⁰
⇒ ∠B = 90⁰ - ∠C
= 90⁰ - 30⁰
= 60⁰
sinB = AC/BC
⇒ AC = BC . sinB
= 12 . sin60⁰
= 6√3 (cm)
sinC = AB/BC
⇒ AB = BC.sinC
= 12.sin30⁰
= 6 (cm)
GIÚP MÌNH VỚI 😭😭😭, bạn nào biết thì trả lời câu hỏi nhanh nhất có thể nha :'((((( . Cho tan a = √3. Tính A = (sin^2a - cos^2a) / (sin a*cos a)
\(tana=\sqrt{3}\)
=>\(\dfrac{sina}{cosa}=\sqrt{3}\)
=>\(sina=\sqrt{3}\cdot cosa\)
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=1+3=4\)
=>\(cos^2a=\dfrac{1}{4}\)
=>\(cosa=\dfrac{1}{2}\)
=>\(sina=\dfrac{\sqrt{3}}{2}\)
\(A=\dfrac{sin^2a-cos^2a}{sina\cdot cosa}\)
\(=\dfrac{\dfrac{3}{4}-\dfrac{1}{4}}{\dfrac{\sqrt{3}}{2}\cdot\dfrac{1}{2}}=\dfrac{2}{4}:\dfrac{\sqrt{3}}{4}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3}\)
