Giả sử pt ax2+bx +c =0
Có 2 nghiệm x1,x2 dương và pt
cx2 + bx +a =0
Cũng có 2 nghiệm x3,x4 dương. Cm rằng x1+x3 lớn hơn hoặc bằng 2
Giả sử pt ax2+bx +c =0
Có 2 nghiệm x1,x2 dương và pt
cx2 + bx +a =0
Cũng có 2 nghiệm x3,x4 dương. Cm rằng x1+x3 lớn hơn hoặc bằng 2
giải gấp giúp mình câu 3 bài 2 với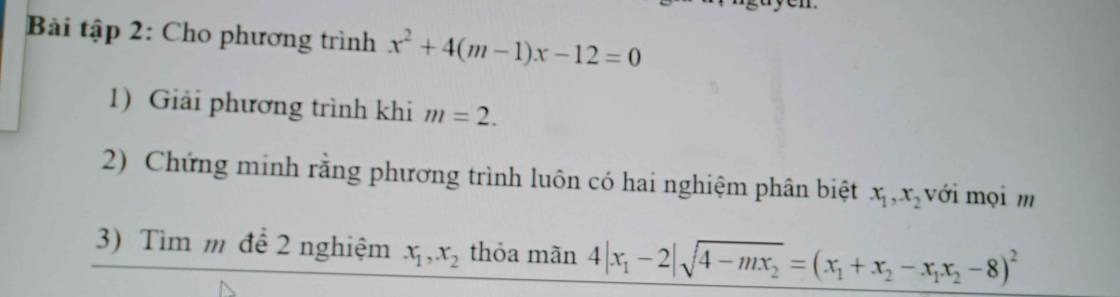
|x1-x2|=2-m
Tìm tất các giá trị của tham số m để phương trình x ^ 2 - 2x - m ^ 2 - 2m - 1 = 0 có hai nghiệm phân biệt x_{1} x_{2} thỏa mãn điều kiện 2x_{1} ^ 2 - x_{2} ^ 2 - x_{1}*x_{2} - 8 = 0
Gọi x1, x2 là 2 nghiệm pb của pt. Tìm m để x1^2 + x2^2 +4
Cho \(x^2\)+\(mx-2=0\)
Tìm m để pt có 2 nghiệm phân biệt sao cho \(x1^3-x2^3=9\)
Cho phương trình: x2 + 3x + m – 1 = 0 (x là ẩn số).
a) Giải phương trình khi m = 3
b) Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn: x1(x14 – 1) + x2(32x24 –1) = 3
Cho x^2-2mx+2-m=0 Tìm giá trị của m để phương trình trên có 2 nghiệm x1 x2 thoả mãn P=(x1.x2)^4+1/16(x1+x2)^4 đạt giá trị nhỏ nhất
jjjj