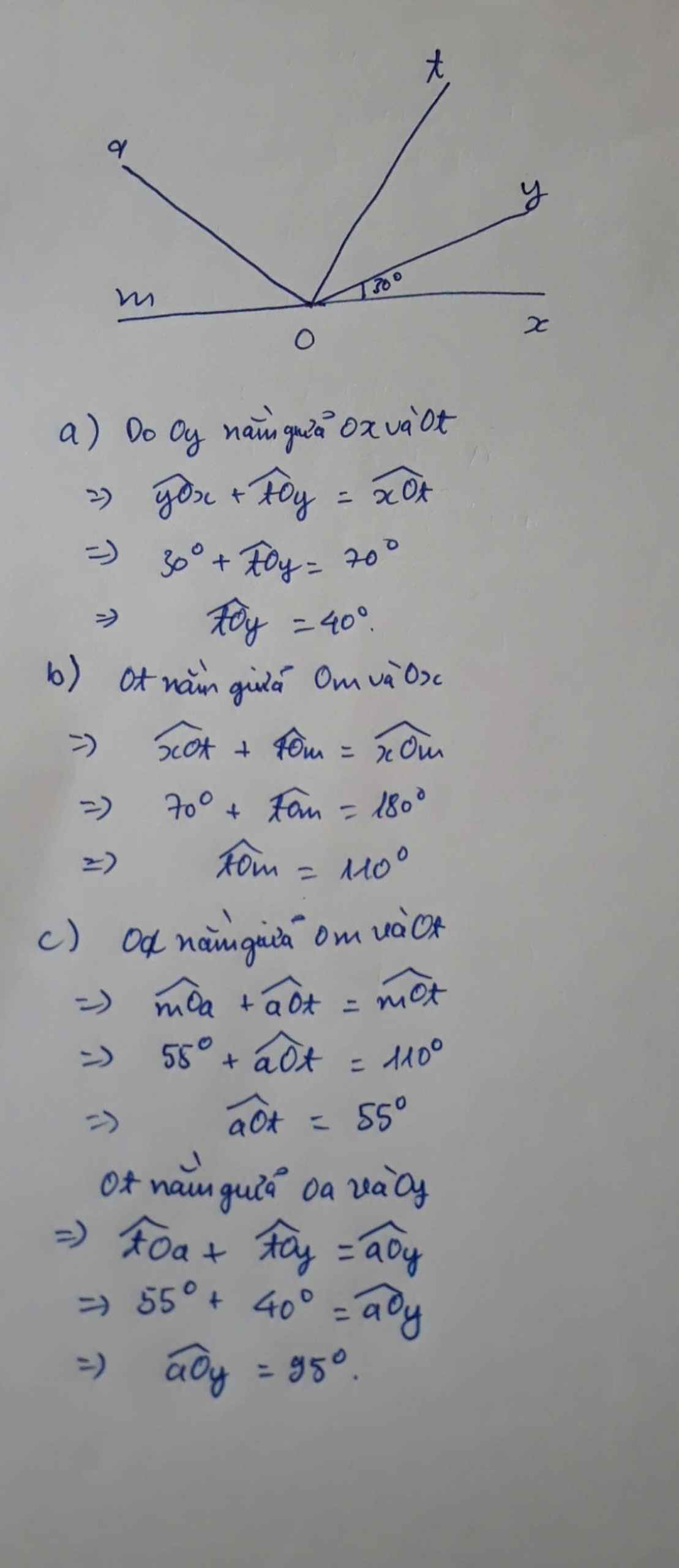Đại số lớp 7

1: Ta có: \(\dfrac{x}{3}=\dfrac{y}{6}\)

mà 4x-y=42

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{3}=\dfrac{y}{6}=\dfrac{4x-y}{4\cdot3-6}=\dfrac{42}{12-6}=\dfrac{42}{6}=7\)

=>\(x=7\cdot3=21;y=6\cdot7=42\)

2: \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}\)

mà x-2y+3z=33

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x-2y+3z}{2-2\cdot3+3\cdot5}=\dfrac{33}{2-6+15}=\dfrac{33}{11}=3\)

=>\(x=3\cdot2=6;y=3\cdot3=9;z=3\cdot5=15\)

3: \(\dfrac{x}{y}=\dfrac{6}{5}\)

=>\(\dfrac{x}{6}=\dfrac{y}{5}\)

mà x+y=121

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{x+y}{6+5}=\dfrac{121}{11}=11\)

=>\(x=11\cdot6=66;y=11\cdot5=55\)

Gọi số đo 3 cạnh trong \(\Delta ABC\) lần lượt là: \(x;y;z\left(^o;x,y,z>0\right)\)
Theo bài ra, ta có:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{7}\) và \(x+y+z=32\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x+y+z}{4+5+7}=\dfrac{32}{16}=2\)
Do đó:
\(\dfrac{x}{4}=2\) nên \(x=2.4=8\)
\(\dfrac{y}{5}=2\) nên \(y=2.5=10\)
\(\dfrac{z}{7}=2\) nên \(z=2.7=14\)
Vậy số đo 3 cạnh trong \(\Delta ABC\) lần lượt là: \(8cm;10cm;14cm\)

Gọi độ dài 3 cạnh của 3 bình lần lượt là: \(a,b,c\)     \(\left(a,b,c\in Z+\right)\)

 \(=>a^3+b^3+c^3=216000\)

Ta có: \(\dfrac{a}{\dfrac{1}{20}}=\dfrac{b}{\dfrac{1}{15}}=\dfrac{c}{\dfrac{1}{12}}\)

\(=>\dfrac{a^3}{\dfrac{1}{8000}}=\dfrac{b^3}{\dfrac{1}{3375}}=\dfrac{c^3}{\dfrac{1}{1728}}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có: 

\(\dfrac{a^3}{\dfrac{1}{8000}}=\dfrac{b^3}{\dfrac{1}{3375}}=\dfrac{c^3}{\dfrac{1}{1728}}=\dfrac{a^3+b^3+c^3}{\dfrac{1}{8000}+\dfrac{1}{3375}+\dfrac{1}{1728}}=\dfrac{216000}{\dfrac{1}{1000}}=216000000\)

\(=>\dfrac{a^3}{\dfrac{1}{8000}}=216000000\)

\(=>a^3=2700\)

\(=>a=30\)

\(=>30.20=15b=12c\)

\(=>15b=12c=600\)

\(=>\left\{{}\begin{matrix}b=40\\c=50\end{matrix}\right.\)

Vậy độ dài 3 cạnh của ba bình cá cảnh lần lượt là: \(30cm;40cm;50cm\)

gọi số học sinh 3 lớp 7A 7B 7C là x y z 

theo bài ra ta có 

x/2=y/2,5=z/3 và x-y=10

áp dụng tính chất dãy tỉ số bằng nhau ta có 

x/2=y/2,5=z/3 =>x/2-z/3=-10

ố thô mk làm vầy vậy bn ghi đề bài có đúng ko

Ta có:

`p^4-q^2(p^2+q^2+1)=(p^2+1)^2`

`<=>[(p^2+1)^2-p^4]+q^2(p^2+q^2+1)=0`

`<=>2p^2+1+q^2p^2+q^4+q^2=0`

`<=>(qp)^2+q^4+2p^2+q^2+1=0`

Với `q=2=>4p^2+16+2p^2+4+1=0`

`<=>6p^2+21=0(L)`

Với `p=2=>4q^2+q^4+8+q^2+1=0`

`<=>q^4+5q^2+9=0(L)`

Với `p,q>2`

`=>p,q` là số lẻ

Ta có: `(2k+1)^2=4k(k+1)+1=>(2k+1)^2` chia 4 dư 1

`=>` SCP lẻ chia 4 dư 1

`(pq)^2, q^4, p^2, q^2` là các SCP lẻ

`=>(pq)^2+q^4+2p^2+q^2+1` chia 4 dư `1+1+2+1+1=6`

`=>(pq)^2+q^4+2p^2+q^2+1` chia 4 dư 2

Mà `0` chia 4 dư 0

Vậy không tồn tại (p;q) thỏa mãn yêu cầu đề bài

Ta có: \(x^2-3xy+y^2\)

\(=x^2-2\cdot x\cdot\frac32y+\left(\frac32y\right)^2-\left(\frac32y\right)^2+y^2\)

\(=\left(x-\frac32y\right)^2-\frac54y^2\)

\(=\left(x-\frac32y-\frac{y\sqrt5}{2}\right)\left(x-\frac32y+\frac{y\sqrt5}{2}\right)\)

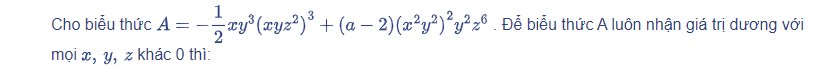
\(A=-\dfrac{1}{2}xy^3\cdot\left(xyz^2\right)^3+\left(a-2\right)\cdot\left(x^2y^2\right)^2\cdot y^2z^6\)

\(=-\dfrac{1}{2}xy^3\cdot x^3y^3z^6+\left(a-2\right)\cdot x^4y^4\cdot y^2z^6\)

\(=-\dfrac{1}{2}x^4y^6z^6+\left(a-2\right)\cdot x^4y^6z^6\)

\(=x^4y^6z^6\left(-\dfrac{1}{2}+a-2\right)=\left(a-\dfrac{5}{2}\right)\cdot x^4y^6z^6\)

Để A>0 với mọi x,y,z khác 0 thì \(a-\dfrac{5}{2}>0\)

=>\(a>\dfrac{5}{2}\)

\(a^2+b^2=c^2\)

\(\Leftrightarrow a^2+b^2+2ab=c^2+2ab\)

\(\Leftrightarrow\left(a+b\right)^2-c^2=2ab\)

\(\Leftrightarrow\left(a+b+c\right)\left(a+b-c\right)=2ab\)

Do \(\left(a+b+c\right)+\left(a+b-c\right)=2\left(a+b\right)\) là 1 số chẵn nên \(a+b+c\) và \(a+b-c\) luôn cùng tính chẵn lẻ

Mà \(2ab\) chẵn \(\Rightarrow\left(a+b+c\right)\left(a+b-c\right)\) chẵn

\(\Rightarrow a+b+c\) và \(a+b-c\) đều chẵn

Do \(a+b-c\) chẵn, đặt \(a+b-c=2k\)

\(\Rightarrow\left(a+b+c\right).2k=2ab\)

\(\Rightarrow\left(a+b+c\right).k=ab\)

\(\Rightarrow a+b+c\) là ước của \(ab\) nên \(ab\) chia hết \(a+b+c\)

\(\left(1-\dfrac{2}{3}-\dfrac{1}{4}\right)\cdot\left(\dfrac{4}{5}-\dfrac{3}{4}\right)\)

\(=\left(\dfrac{12}{12}-\dfrac{8}{12}-\dfrac{3}{12}\right)\cdot\left(\dfrac{16}{20}-\dfrac{15}{20}\right)\)

\(=\dfrac{12-8-3}{12}\cdot\dfrac{16-15}{20}\)

\(=\dfrac{1}{12}\cdot\dfrac{1}{20}\)

\(=\dfrac{1}{12\cdot20}\)

\(=\dfrac{1}{240}\)