Bài 6: Ôn tập chương Tổ hợp - Xác suất

Xung quanh ô quân vua đang đứng có 8 ô, nên ở mỗi một bước, quân vua có 8 cách di chuyển

\(\Rightarrow\) Quân vua có \(8^3\) cách di chuyển 3 bước

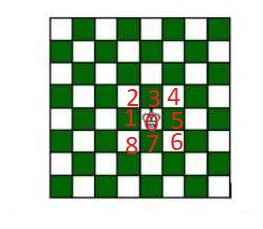
Ở bước đầu tiên, quân vua có 3 kiểu đi: sang các ô xanh hoặc sang các ô đỏ

TH1: quân vua sang ô xanh: có 4 cách. Do vai trò các ô như nhau, giả sử quân vua sang ô số 1

Để sau 2 bước nữa quay về ô 0 ban đầu, ở bước tiếp theo nó phải đi vào 1 ô nằm kế ô 0 \(\Rightarrow\) có 4 cách (là các ô 2,3,7,8)

Vậy có 4.4=16 cách

TH2: Quân vua sang ô trắng (có 4 cách) giả sử là ô số 2, vẫn như trên, bước thứ 2 nó phải sang 1 ô nằm kế ô số 0 => có 2 cách

\(\Rightarrow\) 4.2 =8 cách

Vậy quân vua có \(16+8=24\) cách đi thỏa mãn

Xác suất: \(\dfrac{24}{8^3}=...\)

\(y'=\left(sinx-cosx\right)'.e^{3x}+\left(sinx-cosx\right).\left(e^{3x}\right)'\) 

\(=\left(cosx+sinx\right).e^{3x}+3\left(sinx-cosx\right).e^{3x}\)

\(=4sinx.e^{3x}-2cosx.e^{3x}\)

=>\(\dfrac{\left(n+4\right)!}{\left(n+1\right)!\cdot3!}-\dfrac{\left(n+3\right)!}{n!\cdot3!}=7\left(n+3\right)\)

=>\(\dfrac{\left(n+2\right)\left(n+3\right)\left(n+4\right)}{6}-\dfrac{\left(n+1\right)\left(n+2\right)\left(n+3\right)}{6}=7\left(n+3\right)\)

=>\(\dfrac{\left(n+2\right)\left(n+3\right)\left(n+4-n-1\right)}{6}=7\left(n+3\right)\)

=>\(\left(n+2\right)\left(n+3\right)\cdot3=42\left(n+3\right)\)

=>(n+2)(n+3)=14(n+3)

=>(n+3)(n-12)=0

=>n=12

1: \(\Leftrightarrow n\left(n-1\right)\left(n-2\right)+5\cdot n\left(n-1\right)=2n+30\)

=>n^3-3n^2+2n+5n^2-5n-2n-30=0

=>n^3+2n^2-5n-30=0

=>n=3

2: \(\Leftrightarrow2!\cdot x-3!\cdot x=8\)

=>-2x=8

=>x=-4

3: \(\Leftrightarrow\dfrac{x!}{\left(x-3\right)!}+5\cdot\dfrac{x!}{\left(x-2\right)!}=2x+30\)

=>\(x\left(x-1\right)\left(x-2\right)\)+5x(x-1)=2x+30

=>x=3

4: =>2x^2-6x=8

=>x^2-3x=4

=>x^2-3x-4=0

=>(x-4)(x+1)=0

=>x-4=0

=>x=4

ĐKXĐ: x>=2

PT \(\Leftrightarrow13\cdot\left(\dfrac{x!}{\left(x-2\right)!}+2\cdot\dfrac{x!}{\left(x-1\right)!}\right)-2\cdot\dfrac{\left(x+3\right)!}{\left(x+3-4\right)!\cdot4!}=0\)

\(\Leftrightarrow13\left(x^2-x+2x\right)-2\cdot\dfrac{\left(x+3\right)!}{\left(x-1\right)!\cdot24}=0\)

\(\Leftrightarrow13\left(x^2+x\right)-2\cdot\dfrac{\left(x+3\right)\left(x+2\right)\cdot\left(x+1\right)\cdot x}{24}=0\)

\(\Leftrightarrow13\left(x+1\right)x-\dfrac{1}{12}x\left(x+1\right)\left(x+2\right)\left(x+3\right)=0\)

\(\Leftrightarrow13-\dfrac{1}{12}\left(x+2\right)\left(x+3\right)=0\)

=>1/12(x^2+5x+6)=13

=>x^2+5x+6=156

=>x^2+5x-150=0

=>(x+15)(x-10)=0

=>x=10

Chọn 3 đội xếp vào bảng A: \(C_6^3\) cách

Chọn 3 đội xếp vào bảng B (từ 3 đội còn lại): \(C_3^3\) cách

\(\Rightarrow\) Không gian mẫu: \(C_6^3.C_3^3=20\) cách

Xếp 2 đội HAGL và Thái vào chung 1 bảng: 2 cách (A hoặc B)

Chọn 1 đội xếp vào chung đội với 2 đội nói trên: \(C_4^1=4\) cách

Chọn 3 đội xếp vào bảng còn lại: \(C_3^3=1\) cách

\(\Rightarrow2.4.1=8\) cách xếp 2 đội vào chung bảng

\(\Rightarrow\) Có \(20-8=12\) cách xếp 2 đội vào 2 bảng khác nhau

Xác suất: \(P=\dfrac{12}{20}=\dfrac{3}{5}\)

Mình tự giải được rồi nhé!

Đáp án:

Mỗi xã nhận được 2 tấn lương thực khác loại. Chia quà thành 3 loại khác nhau

- Loại (I): 1 tấn gạo + 1 tấn bột mì

- Loại (II): 1 tấn bột mì + 1 tấn ngô

- Loại (III): 1 tấn ngô + 1 tấn gạo

Đặt a, b, c lần lượt là số loại (I), (II), (III). Theo đề thì:

\(\left\{{}\begin{matrix}a+b=7\\b+c=8\\c+a=5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=2\\b=5\\c=3\end{matrix}\right.\)

Xác suất \(P=\dfrac{C^2_5+C^2_3+C^2_2}{C_{10}^2}=\dfrac{14}{45}\)