=>\(\dfrac{\left(n+4\right)!}{\left(n+1\right)!\cdot3!}-\dfrac{\left(n+3\right)!}{n!\cdot3!}=7\left(n+3\right)\)
=>\(\dfrac{\left(n+2\right)\left(n+3\right)\left(n+4\right)}{6}-\dfrac{\left(n+1\right)\left(n+2\right)\left(n+3\right)}{6}=7\left(n+3\right)\)
=>\(\dfrac{\left(n+2\right)\left(n+3\right)\left(n+4-n-1\right)}{6}=7\left(n+3\right)\)
=>\(\left(n+2\right)\left(n+3\right)\cdot3=42\left(n+3\right)\)
=>(n+2)(n+3)=14(n+3)
=>(n+3)(n-12)=0
=>n=12

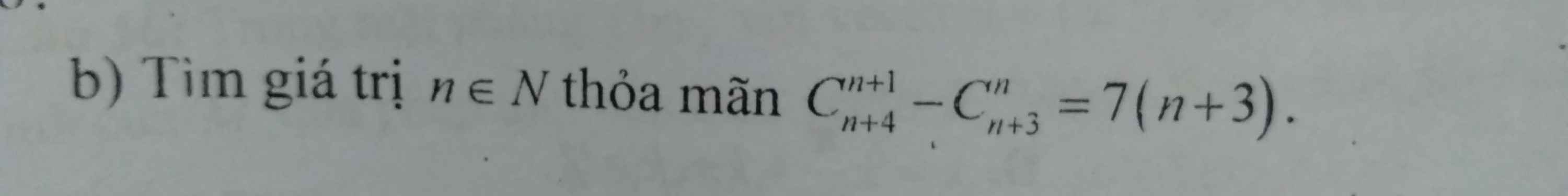






 Giải giúp mình với ạ
Giải giúp mình với ạ


