Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

a: \(\widehat{B}>\widehat{C}\)

nên AB<AC

=>BH<HC

b: Xét ΔDBC có 

BH là hình chiếu của BD trên BC

CH là hình chiếu của CD tren BC

mà HB<HC

nên BD<CD

Câu 1: 

a: Xét Δ​ABC có AB<AC

nên HB<HC

Xét Δ​MBC có

HB là hình chiếu của MB trên BC

HC là hình chiếu của MC trên BC

Do đó: MB<MC(HB<HC)

b: Ta có: Δ​MHB vuông tại H

nên \(\widehat{HMB}< 90^0\)

=>\(\widehat{HMD}>90^0\)

=>DH>DM

Sửa đề: \(5\left(1+\sqrt{1+x^3}\right)=x^2\left(4x^2-25x+18\right)\)

Đặt \(\sqrt{1+x^3}=a>0\)

Thì ta có:

\(5\left(1+a\right)=4x^4-25x^3+18x^2\)

\(\Leftrightarrow4x^4-25a^2+18x^2+20-5a=0\)

\(\Leftrightarrow\left(2x^2-5a+4\right)\left(2x^2+5a+5\right)=0\)

Với \(2x^2+4=5a\)

\(\Leftrightarrow2x^2+4=5\sqrt{1+x^3}\)

\(\Leftrightarrow\left(2x^2+4\right)^2=25\left(1+x^3\right)\)

\(\Leftrightarrow\left(x^2-5x-3\right)\left(4x^2-5x+3\right)=0\)

Tương tự cho trường hợp còn lại.

Xét \(\Delta ABC\) có AB<AC \(\Rightarrow\widehat{ACB}< \widehat{ABC}\)

\(\Rightarrow\widehat{ADC}>\widehat{ADB}\)

a)Gọi H là giao điểm của AI và BC

Xét \(\Delta ABC\) vuông tại A có K là trung điểm BC

\(\Rightarrow KA=KB=KC\)

KA = KB

=> Tam giác KAB cân tại K

\(\Rightarrow\widehat{KAB}=\widehat{KBA}\)

Xét \(\Delta ADE\) vuông tại A có I là trung điểm DE

\(\Rightarrow IA=ID=IE\)

IA = ID

=> Tam giác IAD cân tại I

\(\Rightarrow\widehat{IAD}=\widehat{IDA}\)

\(\widehat{IAB}+\widehat{ABC}=\widehat{IDB}+\widehat{KAB}=90^0\)

Xét \(\Delta ABH\) có :

\(\widehat{IAB}+\widehat{ABC}=90^0\\ \Rightarrow\widehat{AHB}=90^0\\ \Rightarrow AI\perp BC\)

b)

Theo đề ta có :

\(AI\ge AK\\ \Rightarrow DI\ge KC\\ \Rightarrow2.DI\ge2.KC\\ \Rightarrow DE\ge BC\)

Dấu "=" xảy ra khi tam giác ABC vuông cân tại A .

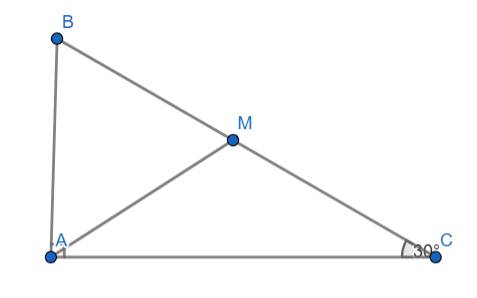
Gọi M là trung điểm của BC 

⇒ AM là đường trung tuyến của BC 

Và ta có: 

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\Rightarrow\widehat{B}=180^o-90^o-30^o=60^o\)

Mà: \(AM=\dfrac{1}{2}BC\Rightarrow AM=BM\)

\(\Rightarrow\Delta ABM\) là tam giác cân 

Lại có \(\widehat{B}=60^o\) khi trong tam giác cân có 1 góc bằng 60 độ thì tam giá đó là tam giác đều 

\(\Rightarrow AM=BM=AB\)

\(\Rightarrow AB=AM=\dfrac{1}{2}BC\left(dpcm\right)\)

Giúp mình nhanh với mình đang gấp lắm rồi

a: Xét tứ giác AMCD có

N là trung điểm của AC

N là trung điểm của MD

Do đó:AMCD là hình bình hành

Suy ra: CD//AM và CD=AM

=>CD//MB và CD=MB

b: Xét ΔABC có 

M là trung điểm của AB

N là trung điểm của AC

Do đó: MN là đường trung bình

=>MN//BC và MN=1/2BC