Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

Em cần giúp gì em ơi?

1:

a: P=6x^2-5x+1-6x^2-2x-7=-7x-6

b: P(2)=-14-6=-20

c: P(x)=0

=>-7x-6=0

=>7x+6=0

=>x=-6/7

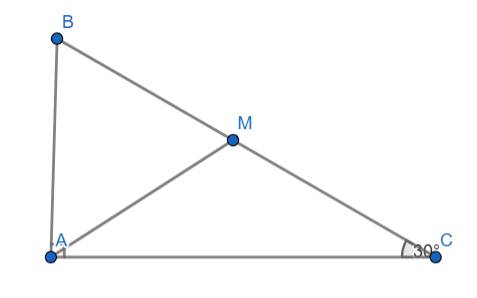
Gọi M là trung điểm của BC 

⇒ AM là đường trung tuyến của BC 

Và ta có: 

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\Rightarrow\widehat{B}=180^o-90^o-30^o=60^o\)

Mà: \(AM=\dfrac{1}{2}BC\Rightarrow AM=BM\)

\(\Rightarrow\Delta ABM\) là tam giác cân 

Lại có \(\widehat{B}=60^o\) khi trong tam giác cân có 1 góc bằng 60 độ thì tam giá đó là tam giác đều 

\(\Rightarrow AM=BM=AB\)

\(\Rightarrow AB=AM=\dfrac{1}{2}BC\left(dpcm\right)\)

Giúp mình nhanh với mình đang gấp lắm rồi

Để chứng minh rằng BD = CE và BD vuông góc với CE, ta sẽ sử dụng một số kiến thức về tam giác và hình học.

a) Để chứng minh BD = CE, ta sẽ sử dụng tính chất của tam giác vuông. Vì AD = AC và góc BAD = góc CAE = 90 độ, nên tam giác ABD và tam giác ACE là hai tam giác vuông cân. Do đó, ta có AB = AC và góc ABD = góc ACE. Từ đó, ta có thể kết luận rằng BD = CE.

b) Để chứng minh BD vuông góc với CE, ta sẽ sử dụng tính chất của đường thẳng vuông góc. Vì AD vuông góc AC và AE vuông góc AB, nên ta có thể kết luận rằng đường thẳng BD là đường thẳng vuông góc với đường thẳng CE.

Với các bước chứng minh trên, ta đã chứng minh được rằng BD = CE và BD vuông góc với CE trong tam giác ABC nhọn.

a: Ta có: \(\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=\widehat{BAC}+90^0\)

\(\widehat{CAD}=\widehat{CAB}+\widehat{DAB}=\widehat{BAC}+90^0\)

Do đó: \(\widehat{BAE}=\widehat{CAD}\)

Xét ΔBAE và ΔDAC có

AB=AD

\(\widehat{BAE}=\widehat{DAC}\)

AE=AC

DO đó: ΔBAE=ΔDAC

=>BE=DC

b: Gọi giao điểm của BE và CD là H

Ta có: ΔBAE=ΔDAC

=>\(\widehat{ABE}=\widehat{ADC};\widehat{AEB}=\widehat{ACD}\)

Xét tứ giác AHBD có \(\widehat{ADH}=\widehat{ABH}\)

nên AHBD là tứ giác nội tiếp

=>\(\widehat{DHA}=\widehat{DBA}=45^0\)

Xét tứ giác AHCE có \(\widehat{AEH}=\widehat{ACH}\)

nên AHCE là tứ giác nội tiếp

=>\(\widehat{AHE}=\widehat{ACE}=45^0\)

\(\widehat{DHE}=\widehat{DHA}+\widehat{EHA}=45^0+45^0=90^0\)

=>EB\(\perp\)CD tại H

Xét ΔDNM có \(\widehat{FNM}\) là góc ngoài tại đỉnh N

nên \(\widehat{FNM}=\widehat{NDM}+\widehat{NMD}=90^0+\widehat{NMD}>90^0\)

Xét ΔFNM có \(\widehat{FNM}\) là góc tù

nên FM là cạnh lớn nhất trong ΔFNM

=>FM>NM

Xét ΔDFM có \(\widehat{FME}\) là góc ngoài tại đỉnh M

nên \(\widehat{FME}=\widehat{MFD}+\widehat{MDF}=90^0+\widehat{MFD}>90^0\)

Xét ΔFME có \(\widehat{FME}>90^0\)

nên FE là cạnh lớn nhất trongΔFME

=>FE>FM

mà FM>NM

nên FE>NM

=>NM<FE

Nó cứ bắt mua vip hỏi à ༎ຶ⁠‿⁠༎ຶ

Hoi nha k phải hỏi 

a: Trên tia BH có HB=HD

nên HB và HD là hai tia đối nhau

mà HB và HC là hai tia đối nhau

nên HD và HC là hai tia trùng nhau

=>\(D\in HC\)

b: Đề sai rồi bạn

a: Xét ΔEMA vuông tại E và ΔFMC vuông tại F có

MA=MC

\(\widehat{AME}=\widehat{CMF}\)(hai góc đối đỉnh)

Do đó: ΔEMA=ΔFMC

=>EM=FM

giúp mk vs nhé

Trong các đường xiên và đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.

Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài 1 đường thẳng đó, đường vuông góc là đường ngắn nhất