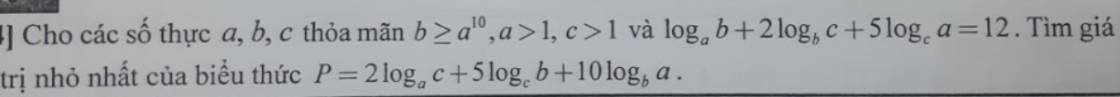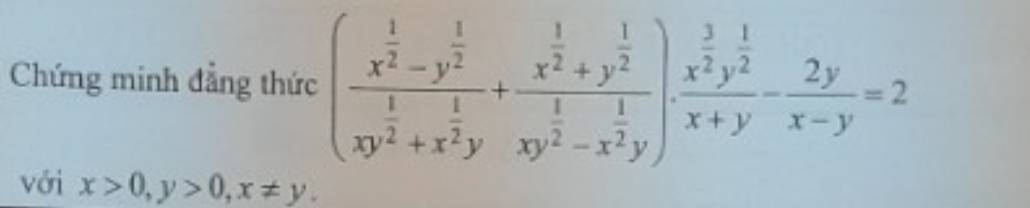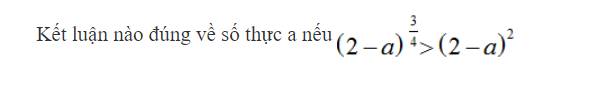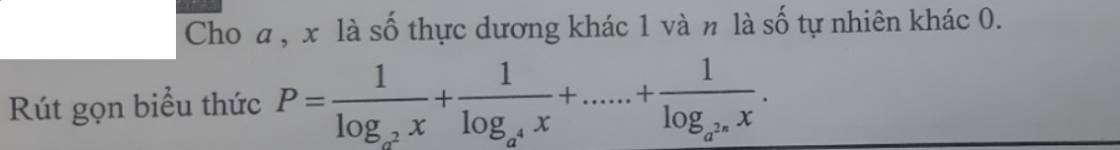Bài 1: Lũy thừa

\(P=\dfrac{a^{\dfrac{1}{3}}\cdot\sqrt{b}+b^{\dfrac{1}{3}}\cdot\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}-\sqrt[3]{ab}\)

\(=\dfrac{a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{2}}+b^{\dfrac{1}{3}}\cdot a^{\dfrac{1}{2}}}{a^{\dfrac{1}{6}}+b^{\dfrac{1}{6}}}-a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}\)

\(=\dfrac{a^{\dfrac{2}{6}}\cdot b^{\dfrac{3}{6}}+a^{\dfrac{3}{6}}\cdot b^{\dfrac{2}{6}}}{a^{\dfrac{1}{6}}+b^{\dfrac{1}{6}}}-a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}\)

\(=\dfrac{a^{\dfrac{2}{6}}\cdot b^{\dfrac{2}{6}}\left(a^{\dfrac{1}{6}}+b^{\dfrac{1}{6}}\right)}{a^{\dfrac{1}{6}}+b^{\dfrac{1}{6}}}-a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}\)

\(=a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}-a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}\)

=0

\(\sqrt{1+\dfrac{1}{x^2}+\dfrac{1}{\left(x+1\right)^2}}=\sqrt{\dfrac{x^2+\left(x+1\right)^2+x^2\left(x+1\right)^2}{x^2\left(x+1\right)^2}}=\sqrt{\dfrac{x^2\left(x+1\right)^2+2x^2+2x+1}{x^2\left(x+1\right)^2}}\)

\(=\sqrt{\dfrac{\left(x^2+x\right)^2+2\left(x^2+x\right)+1}{\left(x^2+x\right)^2}}=\sqrt{\dfrac{\left(x^2+x+1\right)^2}{\left(x^2+x\right)^2}}=\dfrac{x^2+x+1}{x^2+x}\)

\(=1+\dfrac{1}{x}-\dfrac{1}{x+1}\)

\(\Rightarrow f\left(1\right).f\left(2\right)...f\left(2020\right)=5^{1+1-\dfrac{1}{2}+1+\dfrac{1}{2}-\dfrac{1}{3}+...+1+\dfrac{1}{2020}-\dfrac{1}{2021}}\)

\(=5^{2021-\dfrac{1}{2021}}\)

\(\Rightarrow\dfrac{m}{n}=2021-\dfrac{1}{2021}=\dfrac{2021^2-1}{2021}\)

\(\Rightarrow m-n^2=2021^2-1-2021^2=-1\)

Đặt \(\left\{{}\begin{matrix}x=log_ab\ge10\\y=log_bc>0\\z=log_ca>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}xyz=1\\x+2y+5z=12\end{matrix}\right.\) 

\(P=\dfrac{10}{x}+\dfrac{5}{y}+\dfrac{2}{z}=\dfrac{10}{x}+\dfrac{2y+5z}{yz}=\dfrac{10}{x}+x\left(12-x\right)\)

Thật kì lạ, ko hiểu người ta cho điều kiện \(b\ge a^{10}\) làm gì, nó khiến cho P ko tồn tại min (chỉ tồn tại max =21)

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn nhé.

\(log_ab=\dfrac{3}{2}\Rightarrow b=a^{\dfrac{3}{2}}=\left(\sqrt[]{a}\right)^3\)

Do b nguyên \(\Rightarrow\sqrt[]{a}\) nguyên \(\Rightarrow\sqrt[]{a}=x\Rightarrow a=x^2\)

\(log_cd=\dfrac{5}{4}\Rightarrow d=\left(\sqrt[4]{c}\right)^5\Rightarrow\sqrt[4]{c}\) nguyên \(\Rightarrow\sqrt[4]{c}=y\Rightarrow c=y^4\)

\(log_3\left(a-c\right)=2\Rightarrow a-c=9\)

\(\Rightarrow x^2-y^4=9\Rightarrow\left(x-y^2\right)\left(x+y^2\right)=9=1.9=9.1=3.3\)

Pt trên có cặp nghiệm nguyên dương duy nhất \(\left(x;y\right)=\left(5;2\right)\)

\(\Rightarrow log_3\left(b-d\right)=log_3\left(5^3-2^5\right)\)

\(VT=\left(\dfrac{x^{\dfrac{1}{2}}-y^{\dfrac{1}{2}}}{xy^{\dfrac{1}{2}}+x^{\dfrac{1}{2}}y}+\dfrac{x^{\dfrac{1}{2}}+y^{\dfrac{1}{2}}}{xy^{\dfrac{1}{2}}-x^{\dfrac{1}{2}}y}\right)\cdot\dfrac{x^{\dfrac{3}{2}}y^{\dfrac{1}{2}}}{x+y}-\dfrac{2y}{x-y}\)

\(=\left(\dfrac{\sqrt{x}-\sqrt{y}}{x\sqrt{y}+y\sqrt{x}}+\dfrac{\sqrt{x}+\sqrt{y}}{x\sqrt{y}-y\sqrt{x}}\right)\cdot\dfrac{x^{\dfrac{1}{2}}y^{\dfrac{1}{2}}\cdot x}{x+y}-\dfrac{2y}{x-y}\)

\(=\left(\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}+\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}\right)\cdot\dfrac{\sqrt{xy}\cdot x}{x+y}-\dfrac{2y}{x-y}\)

\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\left(\sqrt{x}+\sqrt{y}\right)^2}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+y\right)}\cdot\dfrac{x\sqrt{xy}}{x+y}-\dfrac{2y}{x-y}\)

\(=\dfrac{2\left(x+y\right)}{x-y}\cdot\dfrac{x}{x+y}-\dfrac{2y}{x-y}\)

\(=\dfrac{2x\left(x+y\right)-2y\left(x+y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{2x^2+2xy-2xy-2y^2}{x^2-y^2}\)

\(=\dfrac{2x^2-2y^2}{x^2-y^2}=2\)

Do \(\dfrac{3}{4}\) không nguyên nên trước hết \(2-a>0\Rightarrow a< 2\)

Sau đó \(\left(2-a\right)^{\dfrac{3}{4}}>\left(2-a\right)^2\) mà \(2>\dfrac{3}{4}\Rightarrow2-a< 1\Rightarrow a>1\)

\(\Rightarrow1< a< 2\)

\(P=\dfrac{1}{\dfrac{1}{2}log_ax}+\dfrac{1}{\dfrac{1}{4}log_ax}+...+\dfrac{1}{\dfrac{1}{2n}log_ax}\)

\(=\dfrac{2+4+...+2n}{log_ax}=\dfrac{n\left(n+1\right)}{log_ax}\)

\(log_{ab}b=\dfrac{1}{log_bab}=\dfrac{1}{log_ba+1}=\dfrac{1}{\dfrac{1}{log_ab}+1}=\dfrac{log_ab}{log_ab+1}\)

Đặt \(log_ab=x\) (cho gọn biểu thức)

\(P=\left(x+\dfrac{1}{x}+2\right)\left(x-\dfrac{x}{x+1}\right).\dfrac{1}{x}-1\)

\(=\left(\dfrac{x^2+2x+1}{x}\right)\left(\dfrac{x}{x+1}\right).\dfrac{1}{x}-1\)

\(=\dfrac{x+1}{x}-1=\dfrac{1}{x}=log_ba\)

Pt đầu tương đương: \(\sqrt[3]{x^2}+2\sqrt[3]{y^2}+4\sqrt[3]{z^2}=7\)

Pt 2 tương đương:

\(\left(xy^2+z^4\right)^2-\left(xy^2-z^4\right)^2=4\)

\(\Leftrightarrow4xy^2z^4=4\)

\(\Leftrightarrow xy^2z^4=1\) (1)

Quay lại pt đầu, áp dụng AM-GM:

\(7=\sqrt[3]{x^2}+\sqrt[3]{y^2}+\sqrt[3]{y^2}+\sqrt[3]{z^2}+\sqrt[3]{z^2}+\sqrt[3]{z^2}+\sqrt[3]{z}\ge7\sqrt[7]{\sqrt[3]{x^2}.\sqrt[3]{y^4}.\sqrt[3]{z^8}}\)

\(\Leftrightarrow\sqrt[21]{x^2y^4z^8}\le1\)

\(\Leftrightarrow x^2y^4z^8\le1\)

\(\Rightarrow\left|xy^2z^4\right|\le1\Rightarrow xy^2z^4\le1\)

Dấu "=" xảy ra khi và chỉ khi:

\(\left\{{}\begin{matrix}x^2=y^2=z^2\\xy^2z^4=1\\x>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=\pm1\\z=\pm1\end{matrix}\right.\)

Các bộ thỏa mãn là: \(\left(1;1;1\right);\left(1;1;-1\right);\left(1;-1;1\right);\left(1;-1;-1\right)\)