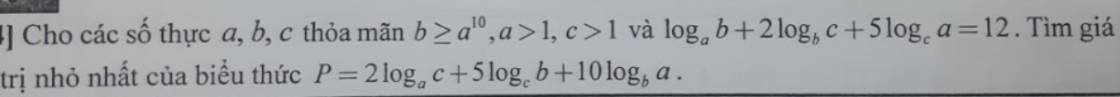Đặt \(\left\{{}\begin{matrix}x=log_ab\ge10\\y=log_bc>0\\z=log_ca>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}xyz=1\\x+2y+5z=12\end{matrix}\right.\)
\(P=\dfrac{10}{x}+\dfrac{5}{y}+\dfrac{2}{z}=\dfrac{10}{x}+\dfrac{2y+5z}{yz}=\dfrac{10}{x}+x\left(12-x\right)\)
Thật kì lạ, ko hiểu người ta cho điều kiện \(b\ge a^{10}\) làm gì, nó khiến cho P ko tồn tại min (chỉ tồn tại max =21)
Đúng 1
Bình luận (8)
