Bài 2: Hàm số lũy thừa
Nội dung lý thuyết
I. KHÁI NIỆM
Hàm số \(y=x^{\alpha}\), với \(\alpha\in R\), được gọi là hàm số luỹ thừa.
Ví dụ: Các hàm số \(y=x;y=x^2;y=\dfrac{1}{x^4};y=x^{\dfrac{1}{3}};y=x^{\sqrt{2}};y=x^{\pi}\) là các hàm số luỹ thừa.
Chú ý: Tập xác định của hàm số luỹ thừa \(y=x^{\alpha}\) tuỳ thuộc vào giá trị của \(\alpha\). Cụ thể:
Với \(\alpha\) nguyên dương, tập xác định là \(R\) ;
Với \(\alpha\) nguyên âm hoặc bằng 0, tập xác định là \(R\backslash\left\{0\right\}\) ;
Với \(\alpha\) không nguyên, tập xác định là \(\left(0;+\infty\right)\).
@40880@
II. ĐẠO HÀM CỦA HÀM SỐ LUỸ THỪA
Hàm số luỹ thừa \(y=x^{\alpha}\) (\(\alpha\in R\)) có đạo hàm với mọi \(x>0\) và
\(\left(x^{\alpha}\right)'=\alpha x^{\alpha-1}\)
Ví dụ 1:
+) \(\left(x^{\dfrac{3}{4}}\right)'=\dfrac{3}{4}.x^{-\dfrac{1}{4}}=\dfrac{3}{4\sqrt[4]{x}}\left(x>0\right)\) ;
+) \(\left(x^{\sqrt{3}}\right)'=\sqrt{3}.x^{\sqrt{3}-1}\left(x>0\right)\)
Chú ý: Công thức tính đạo hàm của hàm hợp đối với hàm số luỹ thừa có dạng:
\(\left(u^{\alpha}\right)'=\alpha u^{\alpha-1}.u'\).
Ví dụ 2:
\(\left(\left(2x^2+x-1\right)^{\dfrac{2}{3}}\right)'=\dfrac{2}{3}.\left(2x^2+x-1\right)^{-\dfrac{1}{3}}.\left(2x^2+x-1\right)'=\dfrac{2\left(4x+1\right)}{3\sqrt[3]{2x^2+x-1}}\)
@29546@
III. KHẢO SÁT HÀM SỐ LUỸ THỪA \(y=x^{\alpha}\)
| \(y=x^{\alpha}\), \(\alpha>0\) | \(y=x^{\alpha}\), \(\alpha< 0\) |
1. Tập khảo sát: \(\left(0;+\infty\right)\) 2. Sự biến thiên: \(y'=\alpha x^{\alpha-1}>0,\forall x>0\) Giới hạn đặc biệt: \(\lim\limits_{x\rightarrow0^+}x^{\alpha}=0,\lim\limits_{x\rightarrow+\infty}x^{\alpha}=+\infty\) Tiệm cận: Không có
3. Bảng biến thiên:
| 1. Tập khảo sát: \(\left(0;+\infty\right)\) 2. Sự biến thiên: \(y'=\alpha x^{\alpha-1}< 0,\forall x>0\) Giới hạn đặc biệt: \(\lim\limits_{x\rightarrow0^+}x^{\alpha}=+\infty,\lim\limits_{x\rightarrow+\infty}x^{\alpha}=0\) Tiệm cận: Trục Ox là tiệm cận ngang ; Trục Oy là tiệm cận đứng của đồ thị 3. Bảng biến thiên:
|
Đồ thị hàm số:

Đồ thị hàm số luỹ thừa \(y=x^{\alpha}\) luôn đi qua điểm \(\left(1;1\right)\).
Chú ý: Khi khảo sát hàm số luỹ thừa với số mũ cụ thể, t phải xét hàm số đó trên toàn bộ tập xác định của nó.
Ví dụ:
+) Đồ thị hàm số \(y=x^3\):

+) Đồ thị hàm số \(y=x^{-2}\):

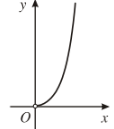
+) Đồ thị hàm số \(y=x^{\pi}\):
Ví dụ 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=x^{-\dfrac{3}{4}}\).
Giải:
1. Tập xác định: \(D=\left(0;+\infty\right)\)
2. Sự biến thiên:
Chiều biến thiên: \(y'=-\dfrac{3}{4}x^{-\dfrac{7}{4}}\)
Do \(y'< 0\) trên khoảng \(\left(0;+\infty\right)\) nên hàm số đã cho nghịch biến
Tiệm cận: \(\lim\limits_{x\rightarrow0^+}y=+\infty\) ; \(\lim\limits_{x\rightarrow+\infty}y=0\).
Đồ thị có tiệm cận ngang là trục hoành và tiệm cận đứng là trục tung.
3. Bảng biến thiên:

4. Đồ thị hàm số:

@2327075@

