Câu 12. (2 điểm) Cho hàm số y = ax bình phương b) Vẽ đồ thị hàm số với giá trị của a vừa tìm được a) Xác định hệ số a, biết rằng đồ thị hàm số đi qua điểm A(3; 2)
Bài 1: Hàm số y = ax^2 (a khác 0)
Thay x=3 và y=2 vào y=ax2, ta được:
9a=2
hay a=2/9
Đúng 0
Bình luận (0)
Đọc tiếp
Bài 1: Cho (P) y=ax^2 (a khác 0) và (d) y=bx+1 1)Tìm a và b để (P) và (d) cùng đi qua M (1;2) Giúp mik vs ạ
Để (P) và (d) cùng đi qua M(1;2) thì
ax^2 = bx+1
<=> a . 1 = b +1
<=> a = b+1
Đúng 1
Bình luận (0)
Giúp mình với 
Phương trình hoành độ giao điểm:
\(\dfrac{1}{2}x^2=\left(m+1\right)x-m\Leftrightarrow x^2-2\left(m+1\right)x+2m=0\) (1)
\(\Delta'=\left(m+1\right)^2-2m=m^2+1>0;\forall m\)
\(\Rightarrow\) (1) luôn có 2 nghiệm pb với mọi m hay (d) và (P) luôn cắt nhau tại 2 điểm với mọi m
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m\end{matrix}\right.\)
Để biểu thức đề bài xác định \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2\ge0\\x_1x_2\ge0\end{matrix}\right.\) \(\Rightarrow m\ge0\)
Khi đó ta có:
\(\sqrt{x_1}+\sqrt{x_2}=2\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=4\)
\(\Leftrightarrow2\left(m+1\right)+2\sqrt{2m}=4\)
\(\Leftrightarrow2m+2\sqrt{2m}-2=0\)
Đặt \(\sqrt{2m}=t\ge0\)
\(\Rightarrow t^2+2t-2=0\Rightarrow\left[{}\begin{matrix}t=-1+\sqrt{3}\\t=-1-\sqrt{3}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2m}=-1+\sqrt{3}\Rightarrow m=2-\sqrt{3}\)
Đúng 1
Bình luận (0)
\(pt\) \(hoành\) \(độ\) \(giao\) \(điểm:\dfrac{1}{2}x^2=\left(m+1\right)x-m\Leftrightarrow x^2-2\left(m+1\right)x+2m=0\)
\(\Delta'=\left(m+1\right)^2-2m=m^2+2m+1-2m=m^2+1>0\left(\forall m\right)\Rightarrowđpcm\)
\(b;\Rightarrow\left\{{}\begin{matrix}x1+x2=2\left(m+1\right)\\x1.x2=2m\end{matrix}\right.\)
\(điều\) \(kiện\) \(tồn\) \(tạicăn\Leftrightarrow0\le x1< x2\Leftrightarrow\left\{{}\begin{matrix}x1.x2\ge0\\x1+x2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m>-1\end{matrix}\right.\)
\(\Leftrightarrow m\ge0\)
\(\Rightarrow\sqrt{x1}+\sqrt{x2}=2\Leftrightarrow x1+x2-2\sqrt{x1x2}=4\)
\(\Leftrightarrow2\left(m+1\right)+2\sqrt{2m}=4\)
\(đặt:\sqrt{2m}=t\ge0\Rightarrow t^2+2t-2=0\Leftrightarrow\left[{}\begin{matrix}t=-1-\sqrt{3}\left(ktm\right)\\t=-1+\sqrt{3}\left(tm\right)\Leftrightarrow m=2-\sqrt{3}\left(tm\right)\end{matrix}\right.\)
\(\Leftrightarrow m=2-\sqrt{3}\left(tm\right)\)
Đúng 1
Bình luận (0)
Cho hàm số Y= 2x2
Tìm tham số m để đường thẳng denta Y=x2 + m - 1 cắt P tại 2 điểm phân biệt
giúp mình với mọi người ơiii
Bạn xem lại ptđt $y=x^2+m-1$ là 1 parabol chứ không phải đường thẳng.
Đúng 0
Bình luận (0)
a: Khi m=4 thì y=2x+3
tan a=2
=>a=63 độ
b: y=mx-2x+3
Tọa độ điểm cố định mà (d) luôn đi qua là:
x=0 và y=-2x+3=3
c: \(d\left(O;d\right)=\dfrac{\left|\left(m-2\right)\cdot0+\left(-1\right)\cdot0+3\right|}{\sqrt{\left(m-2\right)^2+1}}=\dfrac{3}{\sqrt{\left(m-2\right)^2+1}}\)
Để d=1 thì \(\sqrt{\left(m-2\right)^2+1}=3\)
=>(m-2)^2=8
=>\(m=\pm2\sqrt{2}+2\)
Đúng 1
Bình luận (0)

Giúp mình câu b vs ạ
a: 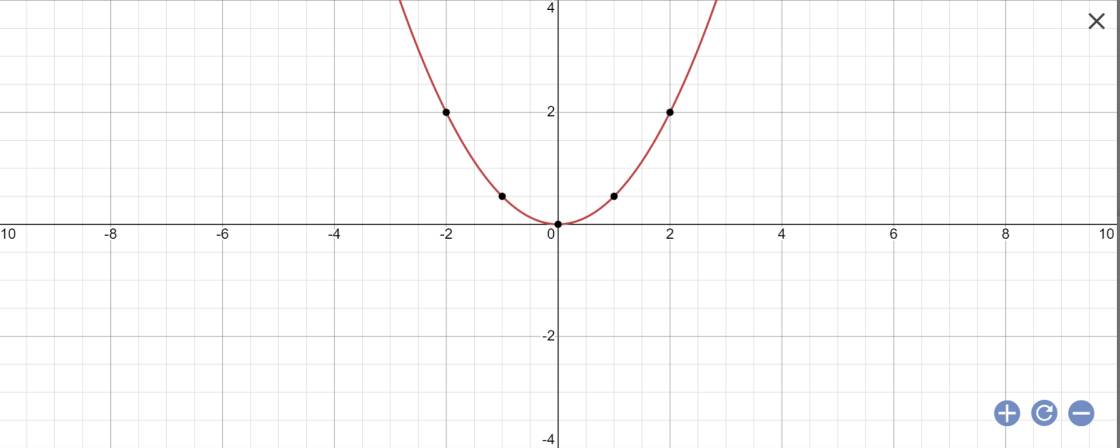
pthđgđ là:
1/2x^2-x-2=0
=>x^2-2x-4=0
=>x^2-2x+1-5=0
=>(x-1)^2=5
=>x=căn 5+1 hoặc x=-căn 5+1
=>y=3+căn 5 hoặc y=3-căn 5
b: C(x;0); D(0;y)
=>vecto CD=(-x;y)
=>vecto DC=(x;-y)
vecto AB=(-2căn 5;-2căn 5)
Để ABCD là hbh thì vecto AB=vecto DC
=>x=-2căn 5 và y=2căn 5
=>C(-2căn5;0); D(0;2căn 5)
Đúng 1
Bình luận (0)
Cho hàm số y = f(x) = \(ax^2\). Biết rằng khi \(x=5\) thì \(y=\dfrac{75}{2}\)
a) Tính giá trị của y khi \(x=-3\).
b) Tìm các giá trị của x khi \(y=15\)
a: f(5)=75/2
=>\(a\cdot5^2=\dfrac{75}{2}\)
=>\(a=\dfrac{75}{2}:25=\dfrac{3}{2}\)
Vậy: \(y=f\left(x\right)=\dfrac{3}{2}x^2\)
Khi x=-3 thì \(y=\dfrac{3}{2}\left(-3\right)^2=\dfrac{3}{2}\cdot9=\dfrac{27}{2}\)
b: y=15
=>\(\dfrac{3}{2}x^2=15\)
=>\(x^2=10\)
=>\(x=\pm\sqrt{10}\)
Đúng 1
Bình luận (0)
Cho hàm số Y =-x2 và hàm sốY=4x2. Tìm giá trị của x để hàm số đồng biến và nghịch biến
*) Hàm số y = -x² có a = -1 < 0
Do đó hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
*) Hàm số y = 4x² có a = 4 > 0
Do đó hàm số đồng biến khi x > 0 và nghịch biến khi x < 0
Đúng 0
Bình luận (0)
Cho hàm số Y= 2x2
Tìm tham số m để đường thẳng denta Y=x2 + m - 1 cắt tại 2 điểm phân biệt
giúp mình với mọi người ơiii
Xét ptr hoành độ của `y=2x^2` và `y=x^2+m-1` có:
`2x^2=x^2+m-1`
`<=>x^2-m+1=0` `(1)`
`2` đường thẳng trên cắt nhau tại `2` điểm pb
`<=>` Ptr `(1)` có `2` nghiệm pb
`<=>\Delta > 0`
`<=>(-m)^2-4.1 > 0`
`<=>m^2 > 4`
`<=>m < -2` hoặc `m > 2`
Đúng 3
Bình luận (0)

























