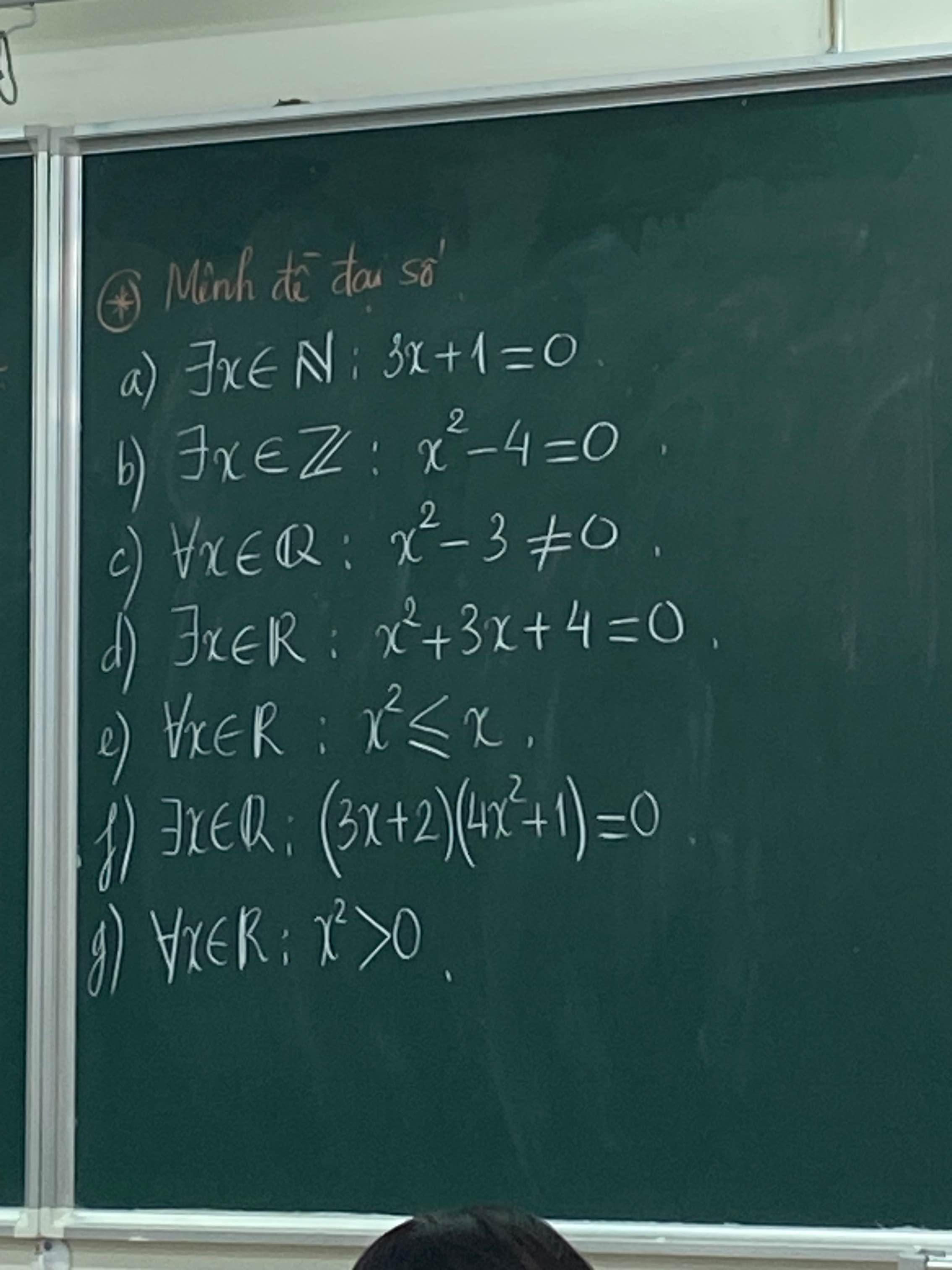a: \(\exists x\in N:3x+1=0\)(7)
3x+1=0
=>3x=-1
=>\(x=-\dfrac{1}{3}\notin N\)
=>Mệnh đề (7) sai
Mệnh đề phủ định là \(\forall x\in R:3x+1\ne0\)
b: \(\exists x\in Z:x^2-4=0\)(6)
\(x^2-4=0\)
=>\(x^2=4\)
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)
=>Mệnh đề (6) đúng
Mệnh đề phủ định là \(\forall x\in Z:x^2-4\ne0\)
c: \(\forall x\in Q:x^2-3\ne0\)(5)
\(x^2-3=0\)
=>\(x^2=3\)
=>\(\left[{}\begin{matrix}x=\sqrt{3}\notin Q\\x=-\sqrt{3}\notin Q\end{matrix}\right.\)
=>Mệnh đề (5) đúng
Mệnh đề phủ định là: \(\exists x\in Q:x^2-3=0\)
d: \(\exists x\in R:x^2+3x+4=0\)(4)
\(x^2+3x+4=0\)
=>\(x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}=0\)
=>\(\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\)(vô lý)
=>Mệnh đề (4) sai
Mệnh đề phủ định là \(\forall x\in R:x^2+3x+4\ne0\)
e: \(\forall x\in R:x^2< =x\left(3\right)\)
Mệnh đề (3) sai vì khi x=2 thì \(x^2=2^2=4;x=2\)
=>\(x^2>x\)
Mệnh đề phủ định là \(\exists x\in R:x^2>x\)
f: \(\exists x\in R:\left(3x+2\right)\left(4x^2+1\right)=0\left(2\right)\)
Mệnh đề (2) đúng vì Khi x=-2/3 thì \(\left(3x+2\right)\left(4x^2+1\right)=\left(3\cdot\dfrac{-2}{3}+2\right)\left[4\cdot\left(-\dfrac{2}{3}\right)^2+1\right]\)
\(=\left(-2+2\right)\left(4\cdot\dfrac{4}{9}+1\right)=0\)
Mệnh đề phủ định là \(\forall x\in R:\left(3x+2\right)\left(4x^2+1\right)\ne0\)
g: \(\forall x\in R:x^2>0\)(1)
Mệnh đề phủ định là \(\exists x\in R:x^2< =0\)
Mệnh đề (1) sai vì khi x=0 thì \(0^2=0\) chứ không phải \(0^2>0\)