D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với 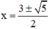
D− thỏa mãn:
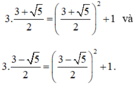
D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với 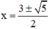
D− thỏa mãn:
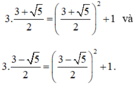
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∀ x ∈ R : x < x + 1
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∃ x ∈ Q : x2 = 2
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó ∀ x ∈ R: x.1 = x;
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó. ∀ x ∈ R: x.x = 1
Cho mênh đề “ ∀ x ∈ ℝ , x 2 + x ≥ − 1 4 ”. Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó
A. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≥ − 1 4 " Đây là mệnh đề đúng
B. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≤ − 1 4 " Đây là mệnh đề đúng
C. A ¯ : " ∃ x ∈ ℝ , x 2 + x < − 1 4 " Đây là mệnh đề đúng
D. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≥ − 1 4 " Đây là mệnh đề sai
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∀ n ∈ N: n chia hết cho n
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó ∀ n ∈ Z: n ≤ n2
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó. Mọi hình vuông đều là hình thoi;
Dùng kí hiệu ∀ và ∃ để viết mệnh đề sau rồi lập mệnh đề phủ định và xét tính đúng sai của mệnh đề đó.
Có một số thực bằng số đối của nó.