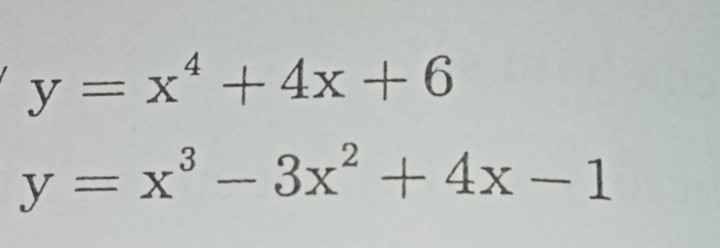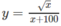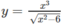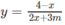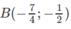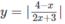TXĐ : D = R
\(y'=4x^3+4=0\Leftrightarrow4\left(x^3+1\right)=0\Leftrightarrow4\left(x+1\right)\left(x^2-x+1\right)=0\Leftrightarrow x=-1\)
Vậy hs nb trên (-vô cùng;-1) ; đb trên (-1;dương vô cùng)
TXĐ : D = R
\(y'=3x^2-6x+4=3\left(x^2-2x+1-1\right)+4=3\left(x-1\right)^2+1>0\)
do y' > 0
nên hs đồng biến trên R