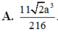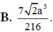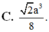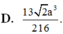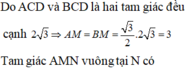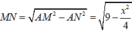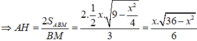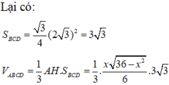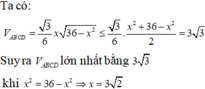Các câu hỏi tương tự
Xét khối tứ diện
A
B
C
D
có cạnh
A
B
x
và các cạnh còn lại đều bằng
2
3
. Tìm
x
để thể tích khối tứ diện
A
B
C
D
đạt giá trị lớn nhất
Đọc tiếp
Xét khối tứ diện A B C D có cạnh A B = x và các cạnh còn lại đều bằng 2 3 . Tìm x để thể tích khối tứ diện A B C D đạt giá trị lớn nhất
![]()
![]()
![]()
![]()
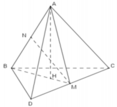
Xét khối tứ diện ABCD có cạnh AB
2
3
và các cạnh còn lại đều bằng x. Tìm x để thể tích khối tứ diện ABCD bằng
2
2
Đọc tiếp
Xét khối tứ diện ABCD có cạnh AB= 2 3 và các cạnh còn lại đều bằng x. Tìm x để thể tích khối tứ diện ABCD bằng 2 2
![]()
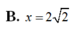
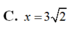
![]()
Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn:
S
A
2
+
S
B
2
18
và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng:
V
m
a
x
x
y
4
;
x...
Đọc tiếp
Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn: S A 2 + S B 2 = 18 và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng: V m a x = x y 4 ; x , y ∈ ℕ * ; (x,y)=1. Khi đó: x, y thỏa mãn bất đẳng thức nào dưới đây?
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có AB x thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất. A.
a
3
3
B.
a
6
4
C.
a
3
4
D....
Đọc tiếp
Cho tứ diện ABCD có AB = x thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.
A. a 3 3
B. a 6 4
C. a 3 4
D. a 6 3
Xét tứ diện ABCD có các cạnh ABBCCDDA1 và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng: A.
2
3
27
B.
4
3
27
C.
2
3
9
D....
Đọc tiếp
Xét tứ diện ABCD có các cạnh AB=BC=CD=DA=1 và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng:
A. 2 3 27
B. 4 3 27
C. 2 3 9
D. 4 3 9
Xét tứ diện ABCD có các cạnh ACCDDBBA2 và AD, BC thay đổi. Giá trị lớn nhất của thể tích tứ diện ABCD bằng: A.
16
3
9
B.
32
3
27
C.
16
3
27
D....
Đọc tiếp
Xét tứ diện ABCD có các cạnh AC=CD=DB=BA=2 và AD, BC thay đổi. Giá trị lớn nhất của thể tích tứ diện ABCD bằng:
A. 16 3 9
B. 32 3 27
C. 16 3 27
D. 32 3 9
Cho tứ diện S.ABC có cạnh SA và tất cả các cạnh còn lại đều bằng 1. Tìm giá trị lớn nhất thể tích tứ diện S.ABC?
Đọc tiếp
Cho tứ diện S.ABC có cạnh SA và tất cả các cạnh còn lại đều bằng 1. Tìm giá trị lớn nhất thể tích tứ diện S.ABC?
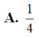
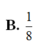
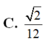
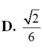
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V . A.
7
2
a
3
216
B.
11...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V .
A. 7 2 a 3 216
B. 11 2 a 3 216
C. 13 2 a 3 216
D. 2 a 3 18
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.