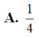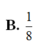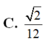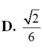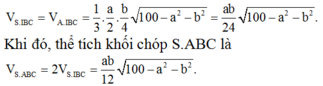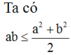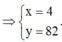Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị của x,y thỏa mãn các bất đẳng thức nào dưới đây? A.
x
2
+
2
x
y
−
y
2
160
B.
x...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị của x,y thỏa mãn các bất đẳng thức nào dưới đây?
A. x 2 + 2 x y − y 2 > 160
B. x 2 − 2 x y + 2 y 2 < 109
C. x 2 + x y − y 4 < 145
D. x 2 − x y + y 4 > 125
Xét khối tứ diện
A
B
C
D
có cạnh
A
B
x
và các cạnh còn lại đều bằng
2
3
. Tìm
x
để thể tích khối tứ diện
A
B
C
D
đạt giá trị lớn nhất
Đọc tiếp
Xét khối tứ diện A B C D có cạnh A B = x và các cạnh còn lại đều bằng 2 3 . Tìm x để thể tích khối tứ diện A B C D đạt giá trị lớn nhất
![]()
![]()
![]()
![]()
Xét khối tứ diện ABCD có cạnh AB x, các cạnh còn lại đều bằng . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất A.
x
6
B.
x
14
C.
x
3
2
D.
x
2
3
Đọc tiếp
Xét khối tứ diện ABCD có cạnh AB = x, các cạnh còn lại đều bằng . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất
A. x = 6
B. x = 14
C. x = 3 2
D. x = 2 3
Cho tứ diện S.ABC, trên cạnh SA và SB lấy điểm M và N sao cho thỏa tỉ lệ
S
M
A
M
1
2
;
S
N
N
B
2
. Mặt phẳng (P) đi qua MN và song song với SC chia tứ diện thành hai khối. Một khối chứa điểm S và có thể tích là V1, khối còn lại c...
Đọc tiếp
Cho tứ diện S.ABC, trên cạnh SA và SB lấy điểm M và N sao cho thỏa tỉ lệ S M A M = 1 2 ; S N N B = 2 . Mặt phẳng (P) đi qua MN và song song với SC chia tứ diện thành hai khối. Một khối chứa điểm S và có thể tích là V1, khối còn lại có thể tích V2. Tỉ số V 1 V 2 nhận giá trị thuộc khoảng nào dưới đây.
![]()
![]()
![]()
![]()
Xét khối tứ diện ABCD có cạnh AB
2
3
và các cạnh còn lại đều bằng x. Tìm x để thể tích khối tứ diện ABCD bằng
2
2
Đọc tiếp
Xét khối tứ diện ABCD có cạnh AB= 2 3 và các cạnh còn lại đều bằng x. Tìm x để thể tích khối tứ diện ABCD bằng 2 2
![]()
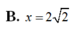
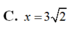
![]()
Cho hình chóp S.ABC có độ dài cạnh SABCx, SBACy, SCABz thỏa mãn điều kiện
x
2
+
y
2
+
z
2
9
. Tính giá trị lớn nhất của thể tích khối chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có độ dài cạnh SA=BC=x, SB=AC=y, SC=AB=z thỏa mãn điều kiện x 2 + y 2 + z 2 = 9 . Tính giá trị lớn nhất của thể tích khối chóp S.ABC
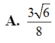
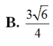
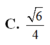
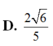
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a 0, b 0, c 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây? A. a + b + c 12 B. a2 + b c - 6 C. a + b + c 18 D. a + b - c 0
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
A. a + b + c = 12
B. a2 + b = c - 6
C. a + b + c = 18
D. a + b - c = 0
Cho hai số dương x, y thỏa mãn
l
o
g
2
(
4
x
+
y
+
2
x
y
+
2
)
y
+
2
8
-
2
x
-
2
y
+
2...
Đọc tiếp
Cho hai số dương x, y thỏa mãn l o g 2 ( 4 x + y + 2 x y + 2 ) y + 2 = 8 - 2 x - 2 y + 2 . Giá trị nhỏ nhất của P = 2 x + y là số có dạng M = a b + c với a , b ∈ ℕ , a > 2 . Tính S = a + b + c
A. 17
B. 7
C. 19
D. 3
Cho tứ diện S.ABC có cạnh SA và tất cả các cạnh còn lại đều bằng 1. Tìm giá trị lớn nhất thể tích tứ diện S.ABC?
Đọc tiếp
Cho tứ diện S.ABC có cạnh SA và tất cả các cạnh còn lại đều bằng 1. Tìm giá trị lớn nhất thể tích tứ diện S.ABC?