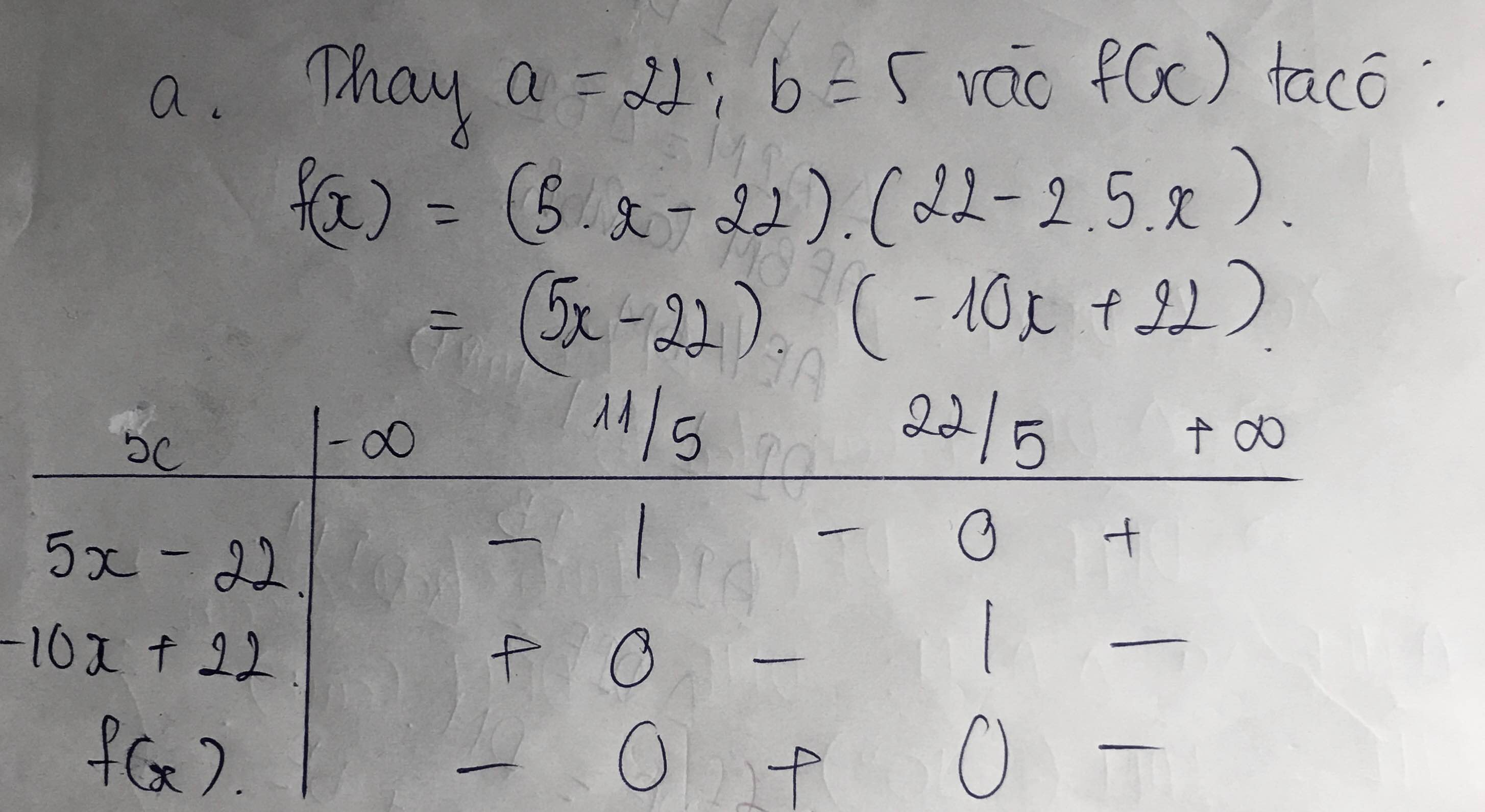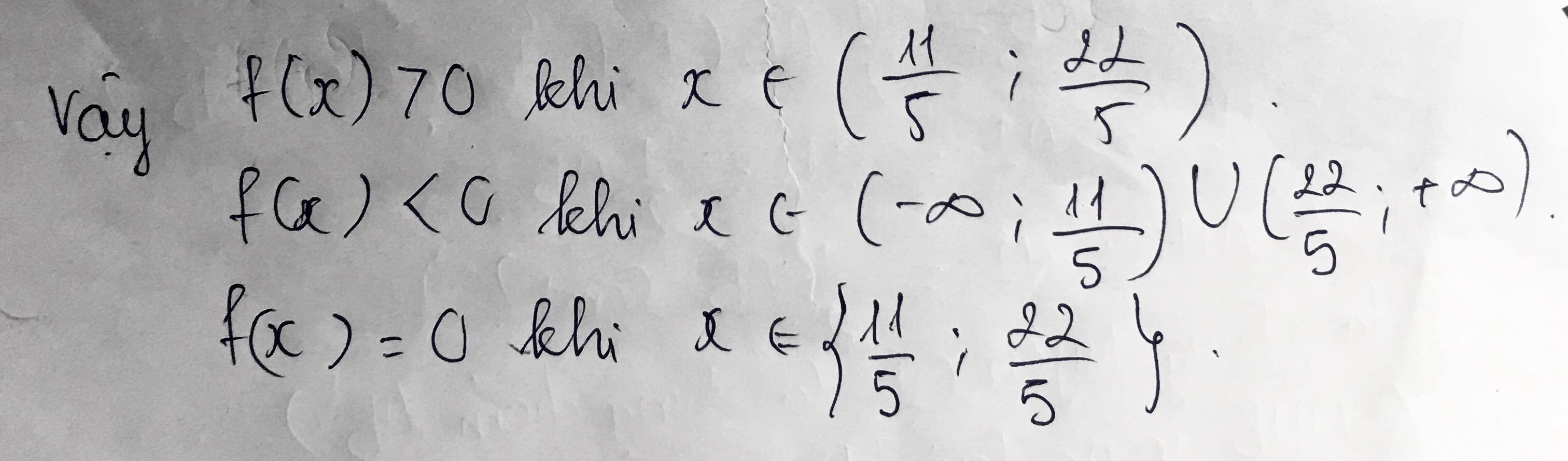Các câu hỏi tương tự
a. Xét dấu của biểu thức f(x) 2x(x+2)-(x+2)(x+1)b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y 2x(x+2) ( C1 ) và y (x+2)(x+1)(C2)Tính tọa độ giao điểm A và B của (C1) và (C2).c. Tính các hệ số a, b, c để hàm số y ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
Đọc tiếp
a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)
b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)
Tính tọa độ giao điểm A và B của (C1) và (C2).
c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
Cho tam thức \(f\left(x\right)=ax^2+bx+c\left(a\ne0\right),\Delta=b^2-4ac\)
Ta có: \(f\left(x\right)\le0.với.\forall x\in R\) khi và chỉ khi?
Giải thích rõ giúp em với ạ, em không hiểu cách xác định dấu:(
Cho đa thức f(x) = a x 2 + bx + c. Xét mệnh đề "Nếu a + b + c = 0 thì f(x) có một nghiệm bằng 1". Hãy phát biểu mệnh đề đảo của mệnh đề đảo của mệnh đề trên. Nêu một điều kiện cần và đủ f(x) có một nghiệm bằng 1
Cho a,b,c là các số thực thỏa mãn a > 0, b > 0 và \(f\left(x\right)=ax^2+bx+c\ge0\)với mọi \(x\in R\). Tìm giá trị nhỏ nhất của biểu thức \(F=\frac{4a+c}{b}\)
Đồ thị hàm số
y
f
(
x
)
a
x
2
+
b
x
+
c
được cho trong hình 47. Kí hiệu
Δ
b
2
-
4
a
c
là biệt số của f(x). Trong các khẳng định sau, kh...
Đọc tiếp
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
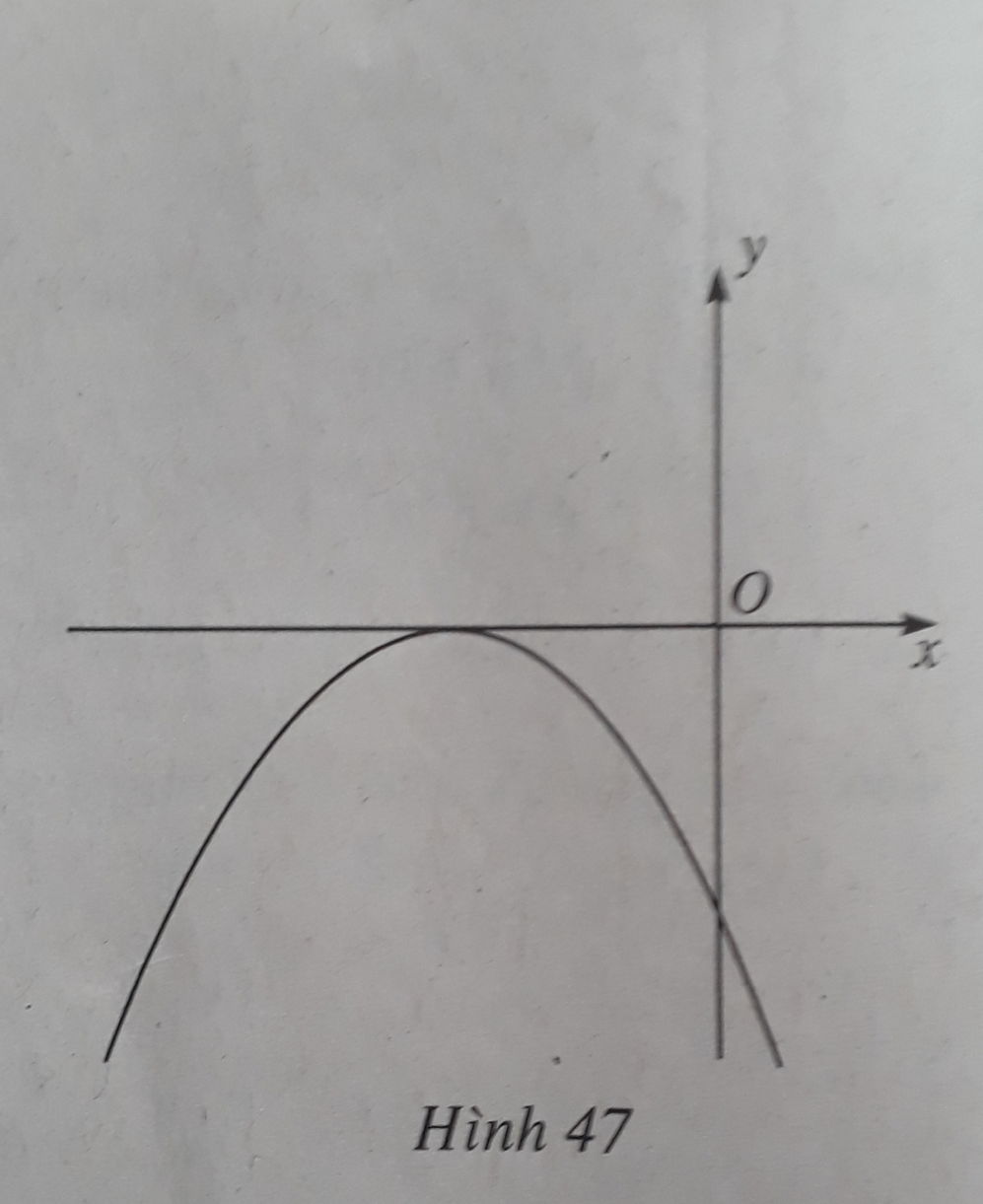
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
Xác định Parabol (P) : y = ax^2 + bx + c ( a khác 0 ) biết (P) đi qua :
a, điểm E (0; 6) và hàm số y = ax^2 - bx + c đạt giá trị nhỏ nhất là 4 khi x = -2
b, điểm F (1; 16) và cắt Ox tại các điểm có hoành độ là -1 và 5.
xét dấu các biểu thức sau
a. f(X)=11X+3/-x2+5x-7
cho tam thức \(f\left(x\right)=ax^2+bx+c\left(a\ne0\right)\), \(\Delta=b^2-4ac\). ta có f(x)>0 với mọi x thuộc r khi và chỉ khi nào
Tam thức bậc hai \(ax^2+bx+c\ge0\)\(\forall x\in R\)và \(b>c>a\).Tìm GTLN:
\(F=\frac{b-c}{9a-2c}+\frac{c-a}{7a-3b+3c}\)