\(P\left(x\right)=\left(x-1\right)\left(x^2+x+1\right)-\left(x-3\right)\left(x-a\right)+3\)
\(=x^3-1-\left(x^2-x\cdot a-3\cdot x+3\cdot a\right)+3\)
\(=x^3-x^2+x\left(a+3\right)-3a+2\)
Để tổng hệ số là 7 thì 1-1+a+3-3a+2=7
=>-2a+5=7
=>-2a=2
=>a=-1
\(P\left(x\right)=\left(x-1\right)\left(x^2+x+1\right)-\left(x-3\right)\left(x-a\right)+3\)
\(=x^3-1-\left(x^2-x\cdot a-3\cdot x+3\cdot a\right)+3\)
\(=x^3-x^2+x\left(a+3\right)-3a+2\)
Để tổng hệ số là 7 thì 1-1+a+3-3a+2=7
=>-2a+5=7
=>-2a=2
=>a=-1
Cho f(x)=\(\left(8x^2+5x-14\right)^{2015}.\left(3x^3-10x^2+6x+2\right)^{2016}\)
Sau khi thu gọn thì tính tổng các hệ số của f(x) là bao nhiêu?
gợi ý: tổng các hệ số trong đa thức 1 biến bằng giá trị của đa thức đó tại giá trị của biến bằng 1
1. Cho đa thức f(x) thỏa mãn (x^2-4x+3) f(x+1)= (x-2) f(x-1). Chứng tỏ rằng đa thức f(x) có ít nhất 3 nghiệm.
2. Đa thức f(x)= ax^2-x+b, a khác 0 có nghiệm x=2. Biết rằng tổng của hệ số cao nhất và hệ số tự do là -7. Tìm a và b
Tìm hệ số a của đa thức
a. A(x) = ax2 + 5x -3, biết rằng đa thức A(x) có 1 nghiệm bằng 1/2
b. B(x) = x3 - ax + 3, biết rằng đa thức B(x) có 1 nghiệm bằng -2
1. Cho đa thức A(x) = ax2 + bx +c (với a,b,c là các hằng số). Chứng minh rằng
a) Nếu a+b+c=0 thì x=1 là một nghiệm của đa thức A(x)
b) Nếu a-b+c=0 thì x=-1 là một nghiệm của đa thức A(x)
2. Cho hai đa thức A(x) và Q(x) đều có nghiệm. Có thể khẳng định được rằng đa thức P(x) + Q(x) luôn có nghiệm hay không? Minh họa cho câu trả lời của em bằng một ví dụ.
3. Cho hai đa thức M(x) và N(x) có cùng một nghiệm. Có thể khẳng định được rằng đa thức M(x) + N(x) luôn có nghiệm hay không? Cho ví dụ minh họa cho câu trả lời của em.
Giúp mình với, mình cần gấp.
1. Cho đa thức A(x) = ax2 + bx +c (với a,b,c là các hằng số). Chứng minh rằng
a) Nếu a+b+c=0 thì x=1 là một nghiệm của đa thức A(x)
b) Nếu a-b+c=0 thì x=-1 là một nghiệm của đa thức A(x)
2. Cho hai đa thức A(x) và Q(x) đều có nghiệm. Có thể khẳng định được rằng đa thức P(x) + Q(x) luôn có nghiệm hay không? Minh họa cho câu trả lời của em bằng một ví dụ.
3. Cho hai đa thức M(x) và N(x) có cùng một nghiệm. Có thể khẳng định được rằng đa thức M(x) + N(x) luôn có nghiệm hay không? Cho ví dụ minh họa cho câu trả lời của em.
Giúp mình với, mình cần gấp.
Trong các số cho sau, với mỗi đa thức, số nào là nghiệm của đa thức ?
a) P(x) = 2x + 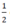 |
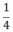 |
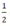 |
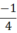 |
| b) Q(x) = x2 – 2x -3 | 3 | 1 | -1 |
Cho các đơn thức: \(2x^6;\) -\(5x^3\); -\(3x^6\); \(x\)\(^3\); - \(\dfrac{3}{5}x^2\); -\(\dfrac{1}{2}x^2\); 8; -\(3x\). Gọi A là tổng của các đơn thức đã cho.
a) tìm tổng A và sắp xếp các hạng tử để được 1 đa thức.
b) tìm hệ số cao nhất, hệ số tự do và hệ số của \(x^2\) của đa thức thu được
Cho đa thức M(x)=x2 - 4x + 4
a,Tính giá trị của đa thức tại x = 1 ;x = 2; x =3 và x = -1
b,Trong các số 1;2;3 và -1 ,số nào là nghiệm của đa thức M(x)
Bài 1: Cho đa thức P(x) và Q(x) là các đơn thức thỏa mãn:
P(x) + Q(x) = x3+x2-4x+2 và P(x) - Q(x) = x3-x2+2x-2
a) Xác định đa thức P(x) và Q(x)
b) Tìm nghiệm của đa thức P(x) và Q(x)
c) Tính giá trị của P(x) và Q(x) biết |x- |\(\dfrac{x}{2}\)- |x-1||| = x-2
Bài 2: Biết rằng P(x) = n.xn+4+ 3.x4-n- 2x3+ 4x- 5 và Q(x) = 3.xn+4- x4+ x3+ 2nx2+ x- 2 là các đa thức với n là 1 số nguyên. Xác định n sao cho P(x) - Q(x) là 1 đa thức bậc 5 và có 6 hạng tử
Bài 3: Cho đa thức P(x) = x+ 7x2- 6x3+ 3x4+ 2x2+ 6x- 2x4+ 1
a) Thu gọn đa thức rồi sắp xếp các số hạng của đa thức theo lũy thừa giảm dần của biến x
b) Xác định bậc của đa thức, hệ số tự do, hệ số cao nhất
c) Tính P(-1); P(0); P(1); P(-a)
Bài 4: Cho đa thức bậc hai P(x) = ax2+ bx+ c với a ≠ 0
a) Chứng tỏ rằng nếu đa thức có nghiệm x = 1 thì sẽ có nghiệm x = \(\dfrac{c}{a}\)
b) Chứng tỏ rằng nếu đa thức có nghiệm x = -1 thì sẽ có nghiệm x = -\(\dfrac{c}{a}
\)
1. Cho đa thức f (x) thỏa mãn ( x2 - 4x + 3) .f ( x + 1 ) = (x - 2).f ( x - 1 ). Chứng tỏ đa thức f (x) có ít nhất 3 nghiệm.
2. Đa thức f (x) = ax2 - x + b, a khác 0 và có nghiệm x = 2. Biết rằng tổng của hệ số cao nhất và hệ sô tự do là -7 . Tìm a và b.