Dễ dàng biến đổi được ![]()
Từ điều kiện, suy ra a > 1
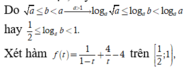 ta được f(t) đạt giá trị nhỏ nhất bằng 5 khi
ta được f(t) đạt giá trị nhỏ nhất bằng 5 khi ![]()
Chọn B.
Dễ dàng biến đổi được ![]()
Từ điều kiện, suy ra a > 1
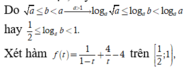 ta được f(t) đạt giá trị nhỏ nhất bằng 5 khi
ta được f(t) đạt giá trị nhỏ nhất bằng 5 khi ![]()
Chọn B.
Cho a,b là các số thực thỏa mãn log 2 . log 2 a - log b = 2 . Hỏi a,b thỏa mãn hệ thức nào dưới đây?
A. a = 100b
B. a = 100 - b
C. a = =100 + b
D. a = 100 b
Xét các số thực a, b thỏa mãn b>1 và a ≤ b < a Biểu thức P = log a b a + 2 log b a b đạt giá trị nhỏ nhất khi
A . a = b 2
B . a 2 = b 3
C . a 3 = b 2
D . a 2 = b
Xét số thực a,b thỏa mãn b>1 và a ≤ b < a . Biểu thức P = log a b a + 2 log b a b đạt giá trị nhỏ nhất khi
A. a = b 2 .
B. a 2 = b 3 .
C. a 3 = b 2 .
D. a 2 = b .
Xét các số phức z = a + bi, (a,b i) thỏa mãn |z – 3 – 3i| = 6. Tính P = 3a + b khi biểu thức 2|z + 6 – 3i| + |z + 1 + 5i| đạt giá trị nhỏ nhất.
A. P = 20
B. P = 2 + 20
C. P = - 20
D. P = - 2 - 20
Xét các số thực a, b thỏa mãn a ≥ b > 1. Biết rằng biểu thức P = 1 log a b a + log a a b đạt giá trị lớn nhất khi b = a k . Khẳng định nào sau đây đúng?
A. k ∈ 2 ; 3
B. k ∈ 3 2 ; 2
C. k ∈ − 1 ; 0
D. k ∈ 0 ; 3 2
Xét các số phức z=a+bi (a,b thuộc R) thỏa mãn |z-3-2i|=2. Tính a+b khi |z+1-2i|+2|z-2-5i| đạt giá trị nhỏ nhất
A. 4 - 3
B. 2 + 3
C. 3
D. 4 + 3
Xét các số phức z=a+bi z = a + b i ( a , b ∈ R ) thỏa mãn z - 3 + 3 i = 2 . Tính P=a+b khi z - 1 + 3 i + z - 3 + 5 i đạt giá trị lớn nhất
A. 2
B. – 2
C. 8
D. – 8
Xét các số phức z = a + b i thỏa mãn z - 3 - 2 i = 2 . Tính a-b biết biểu thức S = z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
A. - 3
B. 3
C. 4
D. 0
Xét các số thực a, b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15