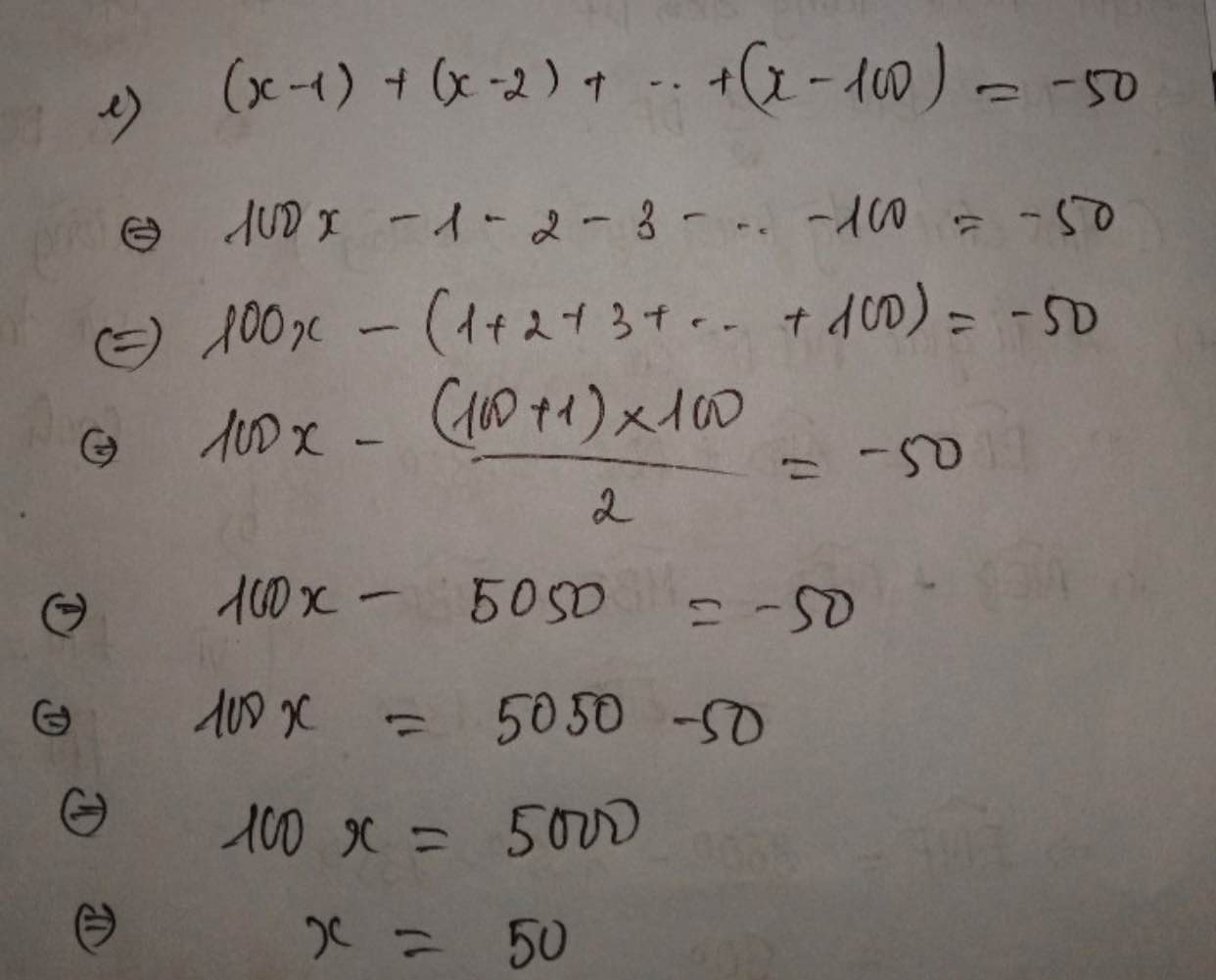Giải:
\(\left(x-1\right)+\left(x-2\right)+...+\left(x-100\right)=-50\)
\(\Rightarrow100x+\left(-1+-2+...+-100\right)=-50\)
\(\Rightarrow100x-\left(1+2+...+100\right)=-50\)
Số số hạng \(\left(1+2+...+100\right)\) là: \(\left(100-1\right):1+1=100\)
Tổng dãy \(\left(1+2+...+100\right)\) là: \(\left(1+100\right).100:2=5050\)
\(\Rightarrow100x-5050=-50\)
\(\Rightarrow100x=-50+5050\)
\(\Rightarrow100x=5000\)
\(\Rightarrow x=5000:100\)
\(\Rightarrow x=50\)
Chúc bạn học tốt!
Ta có: \(\left(x-1\right)+\left(x-2\right)+...+\left(x-100\right)=-50\)
\(\Leftrightarrow100x-5050=-50\)
\(\Leftrightarrow100x=5000\)
hay x=50
Em cảm ơn m.n nhìu ạ!!!
