Đáp án C
Phương pháp: Hàm số y = f(x) nghịch biến trên khoảng
![]() tại hữu hạn điểm thuộc D.
tại hữu hạn điểm thuộc D.
Cách giải:
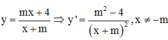
Hàm số y = m x + 4 x + m nghịch biến trên khoảng 1 ; + ∞
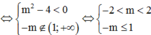
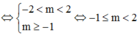
Đáp án C
Phương pháp: Hàm số y = f(x) nghịch biến trên khoảng
![]() tại hữu hạn điểm thuộc D.
tại hữu hạn điểm thuộc D.
Cách giải:
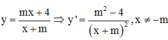
Hàm số y = m x + 4 x + m nghịch biến trên khoảng 1 ; + ∞
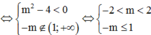
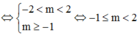
Giá trị nào của m thì hàm số y = x + m x - 2 nghịch biến trên từng khoảng xác định:
A. m < - 2
B. m ≤ - 2
C. m > - 2
D. m ≥ - 2
Với giá trị nào của m thì hàm số y = x 3 + ( m + 1 ) x 2 - ( 3 m + 2 ) x + 4 đồng biến trên khoảng ( 0 ; 1 )
A. m ≤ - 2 3
B. m ≥ - 2 3
C. m ≤ 3
D. m ≥ 3
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x − 1 x − m nghịch biến trên khoảng − ∞ ; 2 .
A. 1 , + ∞
B. 2 , + ∞
C. 2 , + ∞
D. 1 , + ∞
Với giá trị nào của tham số m thì hàm số y = - 1 3 x 3 - m x 2 + 2 m - 3 x - m + 2 nghịch biến trên R?
A. - 3 ≤ m ≤ 1
B. m ≤ 1
C. m ≤ - 3 m ≥ 1
D. - 3 < m < 1
Tất cả giá trị nào của m thì hàm số y = x(m – x2) + m nghịch biến trên khoảng (-1; 1)
A. m < 0
B. m < 3
C. m ≤ 3
D. m ≤ 0
Giá trị nào của m thì hàm số y = x + m x - 2 nghịch biến trên từng khoảng xác định là:
A. m < -2
B. m ≤ - 2
C. m ≥ - 2
D. m > -2
Tìm các giá trị của m để hàm số y = 2 - x - 2 2 - x - m nghịch biến trên khoảng (-1; 1)
A. m ≤ 1 2 , m > 2
B. m ≤ 1 2
C. m > 2
D. m ≤ 2
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên các khoảng mà nó xác định?
A. m ≤ 1 .
B.m<1
C.m<-3
D. m ≤ - 3 .
Cho hàm số y = 2 x + 1 x - m với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng (2;+∞)?
A. 1
B. 2
C. 3
D. 4