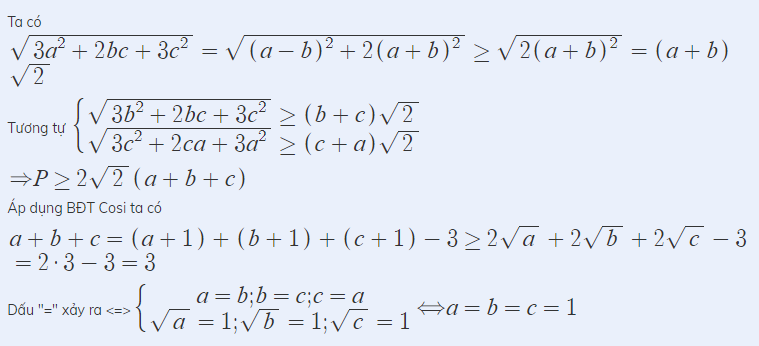Các câu hỏi tương tự
7 tháng 5 2022 lúc 18:39
Cho các số thực a, b, c không âm thỏa \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\). Tìm GTNN của \(P=\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+3c^2}+\sqrt{3c^2+2ca+3a^2}\)
Cho a,b>0 thỏa mãn \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\).Tìm GTNN của
A=\(\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^3+2bc+c^3}+\sqrt{c^3+2ca+a^3}\)
14 tháng 6 2019 lúc 19:36
Cho \(a;b;c\ge0\) thỏa mãn \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)
Tìm giá trị nhỏ nhất của \(P=\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+3c^2}+\sqrt{3c^2+2ca+3a^2}\)
Các bạn giúp mình với.
Giúp mình bài này với ạ :))
Cho các số thực không âm a,b,c thỏa mãn \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)
Tìm giá trị nhỏ nhất của biểu thức P = \(\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+3c^2}+\sqrt{3a^2+2ca+3a^2}\)
Tìm GTLN của B= \(\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+3c^2}+\sqrt{3c^2+2ac+3a^2}\)
Biết a,b,c >=0 và \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)3
1 . )
Cho 3 số a,b,c dương. Tìm giá trị lớn nhất của biểu thức
\(P=\frac{a}{2a+b+c}+\frac{b}{2b+c+a}+\frac{c}{2c+a+b}\)
2
cho các số thực không âm a,b,c thỏa mãn \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)
Tìm giá trị nhỏ nhất của biểu thức
\(\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+3c^2}+\sqrt{3c^2+2ca+3a^2}\)
27 tháng 10 2021 lúc 9:08
Cho các số thực dương a, b, c thỏa mãn a + b + c = 3. Chứng minh rằng:\(\sqrt{a^2+3b^2}+\sqrt{b^2+3c^2}+\sqrt{c^2+3a^2}\ge6\)
a,b,c là các số thực không âm thỏa mãn a+b+c=2. Tìm max và min của \(P=\sqrt{a+b^3c^3}+\sqrt{b+c^3a^3}+\sqrt{c+a^3b^3}\)
Cho a,b,c>0,tim GTNN:\(\frac{\sqrt{a^3c}}{\sqrt{b^3a}+bc}+\frac{\sqrt{b^3a}}{\sqrt{c^3b}+ac}+\frac{\sqrt{c^3b}}{\sqrt{a^3c}+ab}\)