\(y=\dfrac{x+9}{x+1}\)
=>\(y'=\dfrac{\left(x+9\right)'\left(x+1\right)-\left(x+9\right)\left(x+1\right)'}{\left(x+1\right)^2}\)
=>\(y'=\dfrac{x+1-x-9}{\left(x+1\right)^2}=-\dfrac{8}{\left(x+1\right)^2}\)
Gọi phương trình tiếp tuyến cần tìm là (d): y=ax+b
Δ: x-2y+2=0
=>2y=x+2
=>\(y=\dfrac{1}{2}x+1\)
Vì Δ\(\perp\)(d) nên \(a\cdot\dfrac{1}{2}=-1\)
=>a=-2
Vậy: (d): y=-2x+b
(d) là tiếp tuyến của (C)
=>\(-\dfrac{8}{\left(x+1\right)^2}=-2\)
=>\(\left(x+1\right)^2=4\)
=>\(\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
TH1: x=1
\(y=\dfrac{1+9}{1+1}=\dfrac{10}{2}=5;y'=\dfrac{-8}{\left(1+1\right)^2}=-2\)
Phương trình tiếp tuyến là:
y=-2(x-5)=-2x+10
TH2: x=-3
\(y=\dfrac{-3+9}{-3+1}=\dfrac{6}{2}=3\)
Phương trình tiếp tuyến là:
y=-2(x-3)=-2x+6
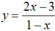.Viết phương trình tiếp tuyến với đồ thị hàm số biết tiếp tuyến vuông góc với đường thẳng d : x – y + 2017 = 0
.
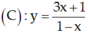
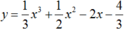