\(\dfrac{7}{9}=\dfrac{28}{36};\dfrac{5}{12}=\dfrac{15}{36}\)
\(\dfrac{28}{36}\) ; \(\dfrac{15}{36}\)
\(\dfrac{7}{9}=\dfrac{28}{36};\dfrac{5}{12}=\dfrac{15}{36}\)
\(\dfrac{7}{9}=\dfrac{28}{36};\dfrac{5}{12}=\dfrac{15}{36}\)
\(\dfrac{28}{36}\) ; \(\dfrac{15}{36}\)
\(\dfrac{7}{9}=\dfrac{28}{36};\dfrac{5}{12}=\dfrac{15}{36}\)
viết các phân số lần lượt bằng 11/13 , 9/11 và có MSC là 143
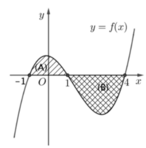
Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ bên. Biết rằng diện tích các hình phẳng (A), (B) lần lượt bằng 3 và 7. Tích phân ∫ 0 π 2 cos x , f ( 5 sin x - 1 ) d x bằng
A. - 4 5
B. 2
C. 4 5
D. -2
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có đồ thị như hình vẽ bên.
và có đồ thị như hình vẽ bên.
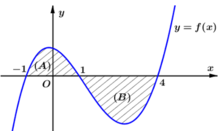
Biết rằng diện tích hình phẳng ![]() ,
, ![]() lần lượt bằng 3 và 7. Tích phân
lần lượt bằng 3 và 7. Tích phân 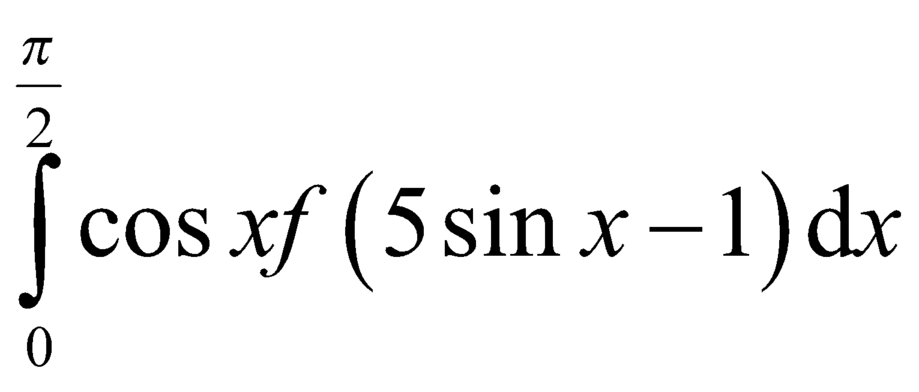 bằng
bằng
A. ![]() .
.
B. 2.
C.![]() .
.
D.-2.
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số
y = log a x , y = log a x , y = log a 3 x , với x > 0 , a > 1 .
Giá trị của a là:
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6
Cho hình vuông ABCD có diện tích bằng 36, A B → là một vectơ chỉ phương của đường thẳng y=0, các điểm A, B, C lần lượt nằm trên đồ thị hàm số y = log a x , y = 2 log a x , y = 3 log a x . Tìm a.
![]()
![]()
![]()
![]()
Đồ thị hàm số y = 1 - 3 x 2 x 2 - 6 x + 9 có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A. x = 3 và y = -3.
B. x = 3 và y = 0.
C. x = 3 và y = 1.
D. y = 3 và x = -3.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số V ' V có giá trị nhỏ nhất bằng
A. 1 5
B. 3 8
C. 1 3
D. 1 2
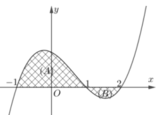
Cho hàm số y = f ( x ) liên tục trên R và có đồ thị như hình vẽ. Biết rằng diện tích các hình phẳng (A), (B) lần lượt bằng 15 và 3. Tích phân ∫ 1 e 1 1 x . f ( 3 ln x + 2 ) d x bằng
![]()
![]()
![]()
![]()