
Vẽ hộ em hình ạ.
I'm unable to draw images, but I can help you understand how to approach creating the diagram based on the text. Here's the transcribed text from the image:
---
Câu 3. (2,5 điểm): Cho đường tròn \((O; R)\). Từ điểm \(A\) trên đường tròn \((O)\), kẻ tiếp tuyến \(d\) với \((O)\). Trên đường thẳng \(d\) lấy điểm \(M\) bất kỳ \((M\) khác \(A\)). Kẻ tiếp tuyến \(MB\) với đường tròn \((O)\) \((B\) là tiếp điểm).
a) Chứng minh bốn điểm \(A, M, B, O\) cùng thuộc một đường tròn.
b) Từ \(A\) kẻ \(AC \perp MB\) \((C \in BM)\). Từ \(B\) kẻ \(BD \perp AM\) \((D \in AM)\). Gọi \(H\) là giao điểm của \(AC\) và \(BD\), \(I\) là giao điểm của \(OM\) và \(AB\). Chứng minh rằng: \(OI \cdot OM = R^2\) và \(OI \cdot IM = IA^2\).
c) Chứng minh ba điểm \(O, H, M\) thẳng hàng.
---
To draw the diagram:
1. Draw a circle with center \(O\) and radius \(R\).
2. Place point \(A\) on the circle.
3. Draw tangent line \(d\) from point \(A\).
4. Choose any point \(M\) on line \(d\) (other than \(A\)).
5. Draw tangent \(MB\) to the circle, with \(B\) as the point of tangency.
6. Draw perpendicular \(AC\) from \(A\) to \(MB\) and mark \(C\) on \(BM\).
7. Draw perpendicular \(BD\) from \(B\) to \(AM\) and mark \(D\) on \(AM\).
8. Mark intersection \(H\) of \(AC\) and \(BD\).
9. Mark intersection \(I\) of \(OM\) and \(AB\).
10. Verify and label all relevant points and lines.
This
a: Xét tứ giác AMBO có \(\hat{MAO}+\hat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra MO là đường trung trực của AB
=>MO⊥AB tại I
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot OM=OA^2=R^2;IO\cdot IM=IA^2\)
c: Xét ΔDAB vuông tại D và ΔCBA vuông tại C có
BA chung
\(\hat{DAB}=\hat{CBA}\) (ΔMAB cân tại M)
Do đó: ΔDAB=ΔCBA
=>\(\hat{DBA}=\hat{CAB}\)
=>\(\hat{HAB}=\hat{HBA}\)
=>HA=HB
=>H nằm trên đường trung trực của AB(3)
Từ (1),(2),(3) suy ra O,H,M thẳng hàng






 vẽ hình hộ thôi ạ
vẽ hình hộ thôi ạ





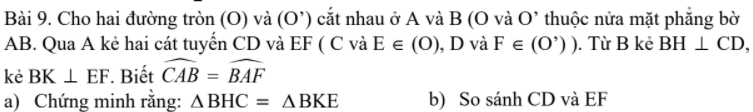

 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ


