\(a,\Delta ABC\text{ cân }A\Rightarrow AH\text{ cũng là trung tuyến}\\ \left\{{}\begin{matrix}BH=HC\\AH=HE\end{matrix}\right.\Rightarrow ABEC\text{ là hbh}\\ \text{Mà }AE\bot BC=\left\{H\right\}\Rightarrow ABEC\text{ là hình thoi}\\ b,\text{Vì }D,F\text{ là trung điểm }AH,HC\Rightarrow DF\text{ là đtb }\Delta AHC\\ \Rightarrow DF=\dfrac{1}{2}AC\\ \text{Xét }\Delta AHC\bot H\Rightarrow HI=\dfrac{1}{2}AC\left(\text{trung tuyến ứng cạnh huyền }\right)\\ \Rightarrow DF=HI\)
a: Xét tứ giác ABEC có
H là trung điểm của AE
H là trung điểm của BC
Do đó: ABEC là hình bình hành
mà AB=AC
nên ABEC là hình thoi













 Vẽ hình và giải chi tiết giúp em với ạ Cảm ơn mọi người nhiều ạ
Vẽ hình và giải chi tiết giúp em với ạ Cảm ơn mọi người nhiều ạ Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ

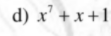

 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn

