Bài 1:
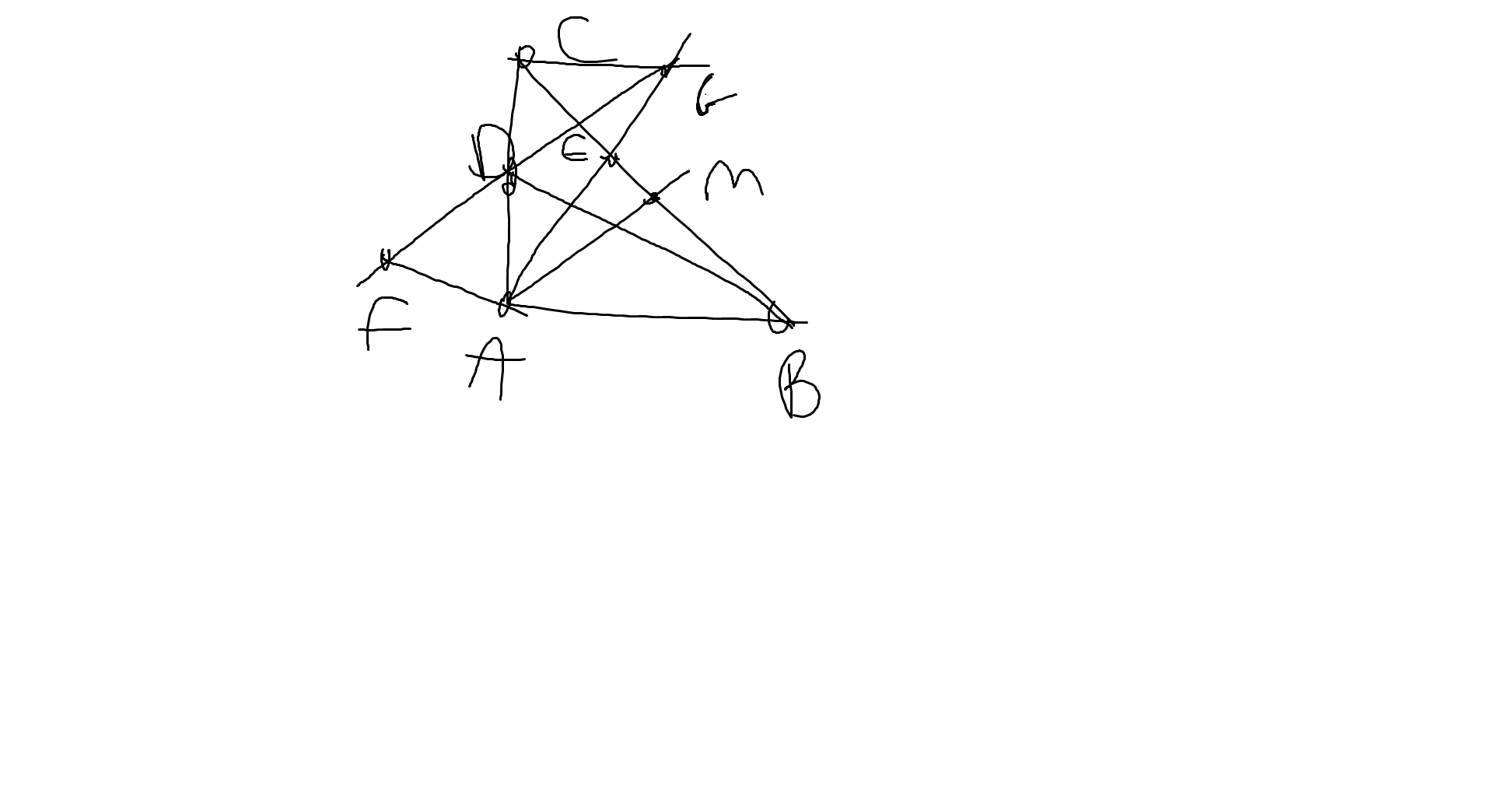
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
b: Xét ΔADF và ΔCDE có
DA=DC
\(\widehat{ADF}=\widehat{CDE}\)(hai góc đối đỉnh)
DF=DE
Do đó: ΔADF=ΔCDE
=>\(\widehat{DAF}=\widehat{DCE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//CE
c: Xét ΔBAD vuông tại A và ΔACG vuông tại C có
BA=AC
\(\widehat{ABD}=\widehat{CAG}\left(=90^0-\widehat{GAB}\right)\)
Do đó: ΔBAD=ΔACG
d: ΔBAD=ΔACG
=>AD=CG
mà \(AD=\dfrac{AC}{2}\)
và AB=AC
nên \(CG=\dfrac{AB}{2}\)
=>AB=2CG
Bài 2:
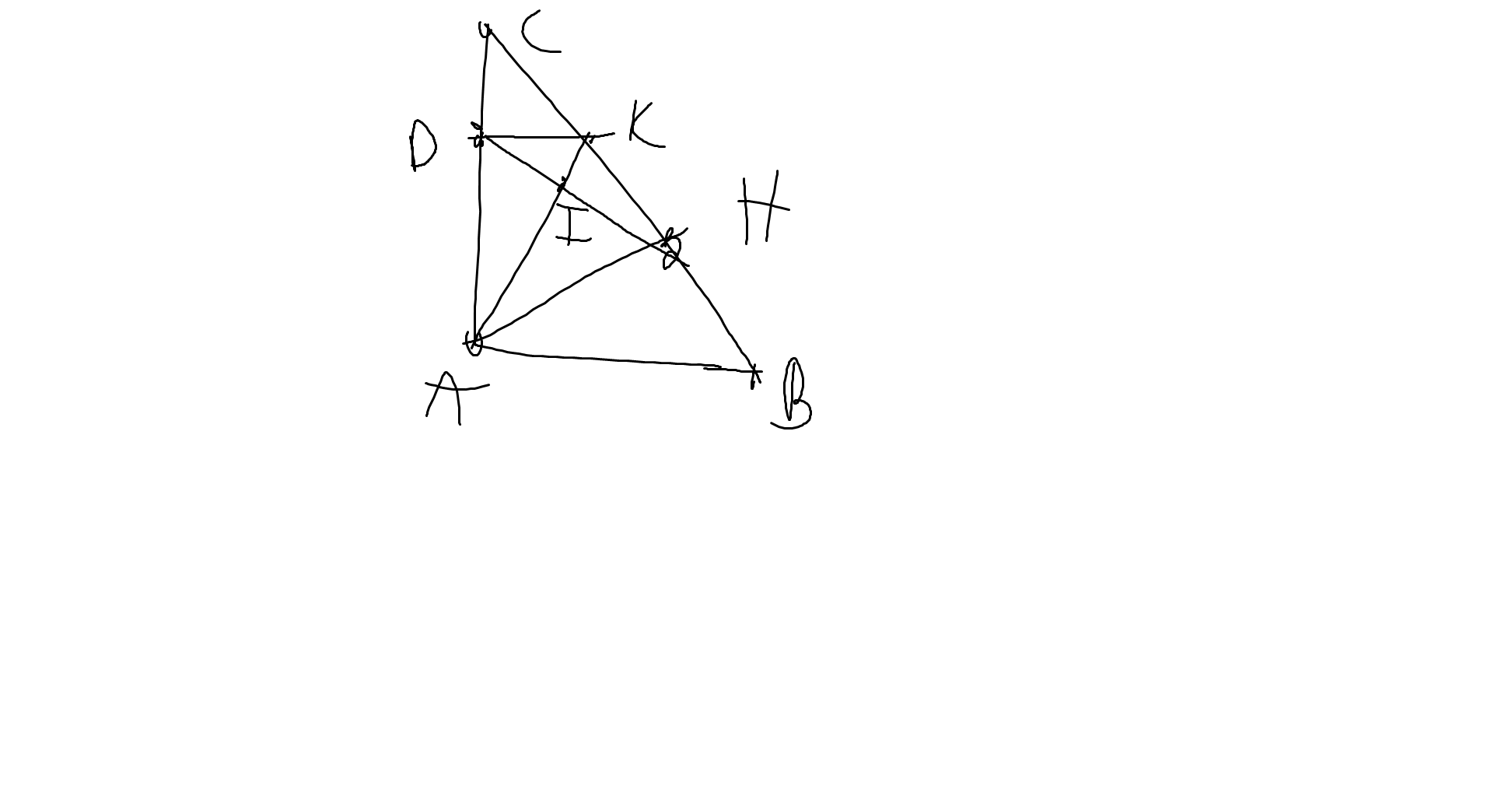
a:ΔHAB vuông tại H
=>\(\widehat{HAB}+\widehat{HBA}=90^0\)
=>\(\widehat{HAB}=90^0-60^0=30^0\)
b: Xét ΔAHI và ΔADI có
AH=AD
HI=DI
AI chung
Do đó: ΔAHI=ΔADI
c: ΔAHI=ΔADI
=>\(\widehat{HAI}=\widehat{DAI}\)
Xét ΔAHK và ΔADK có
AH=AD
\(\widehat{HAK}=\widehat{DAK}\)
AK chung
Do đó: ΔAHK=ΔADK
=>\(\widehat{AHK}=\widehat{ADK}\)
=>\(\widehat{ADK}=90^0\)
=>DK\(\perp\)AC
Bài 3:
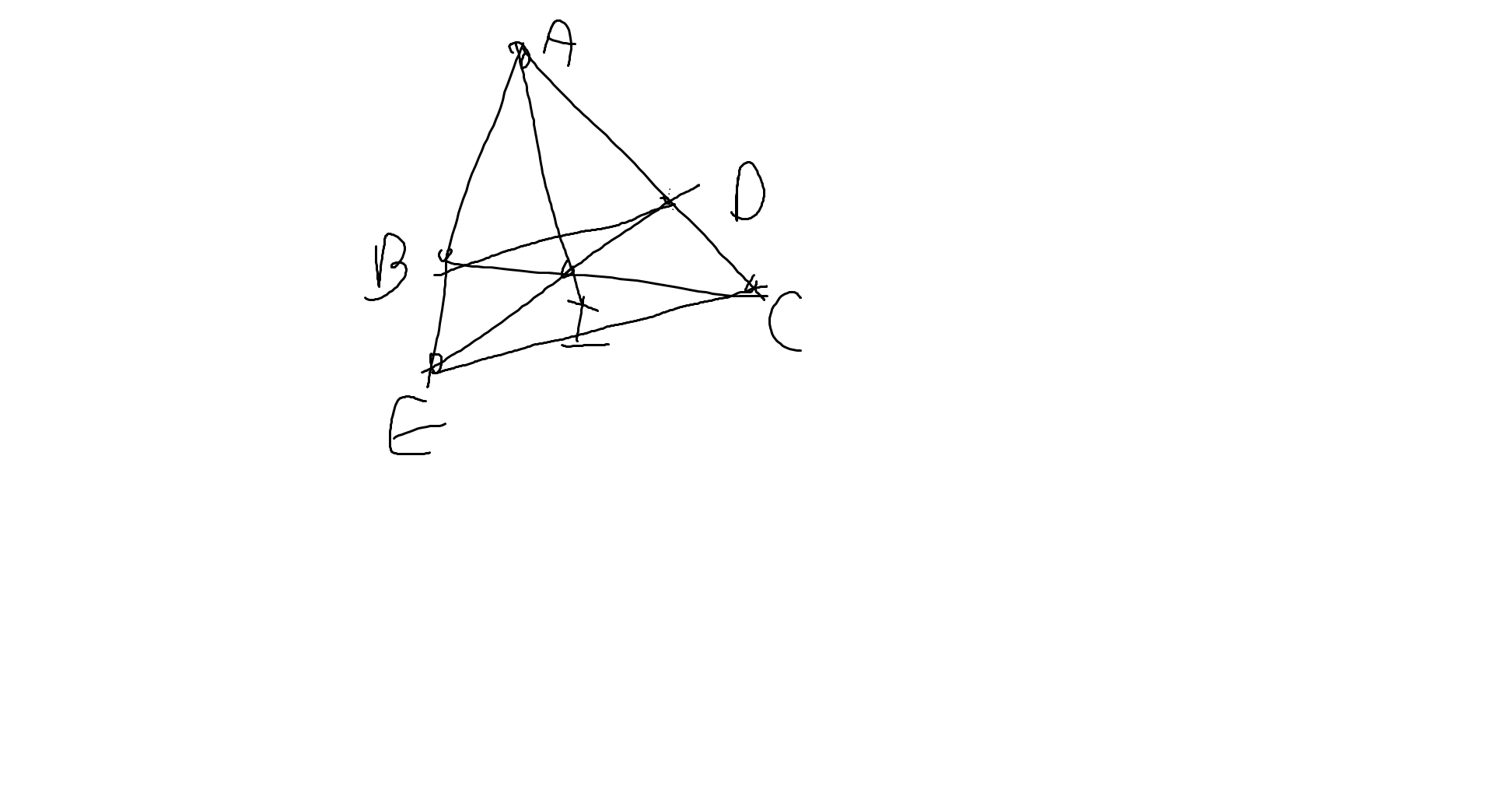
a: Xét ΔABI và ΔADI có
AB=AD
\(\widehat{BAI}=\widehat{DAI}\)
AI chung
Do đó: ΔAIB=ΔAID
=>IB=ID
b: Ta có: ΔAIB=ΔAID
=>\(\widehat{ABI}=\widehat{ADI}\)
mà \(\widehat{ABI}+\widehat{IBE}=180^0\)(hai góc kề bù)
và \(\widehat{ADI}+\widehat{CDI}=180^0\)(hai góc kề bù)
nên \(\widehat{IBE}=\widehat{IDC}\)
Xét ΔIBE và ΔIDC có
\(\widehat{IBE}=\widehat{IDC}\)
IB=ID
\(\widehat{BIE}=\widehat{DIC}\)(hai góc đối đỉnh)
Do đó: ΔIBE=ΔIDC
c: ΔIBE=ΔIDC
=>BE=DC và \(\widehat{IEB}=\widehat{ICD}\)
Xét ΔAEC có \(\dfrac{AB}{BE}=\dfrac{AD}{DC}\)
nên BD//EC
c: Ta có: \(\widehat{ABC}=2\cdot\widehat{ACB}\)
=>\(\widehat{ABI}=2\cdot\widehat{BEI}\)
Xét ΔIEB có \(\widehat{ABI}\) là góc ngoài tại đỉnh B
nên \(\widehat{ABI}=\widehat{BIE}+\widehat{BEI}\)
=>\(2\cdot\widehat{BEI}=\widehat{BIE}+\widehat{BEI}\)
=>\(\widehat{BIE}=\widehat{BEI}\)
=>BI= BE
AB+BI=AB+BE=AE
mà AE=AC
nên AB+BI=AC
Vẽ hộ mình cả hình nữa với! Mình cảm ơn nhiều
Vẽ hình giúp mình với,mình cần gấp.
