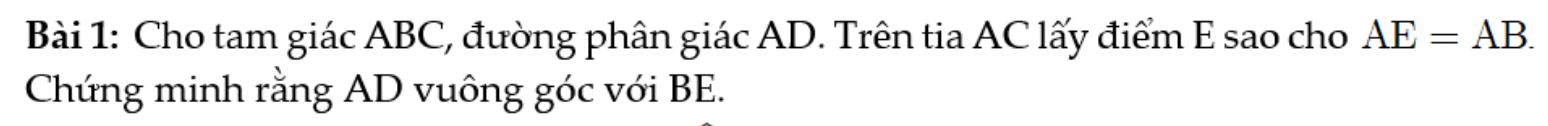Bài 5:
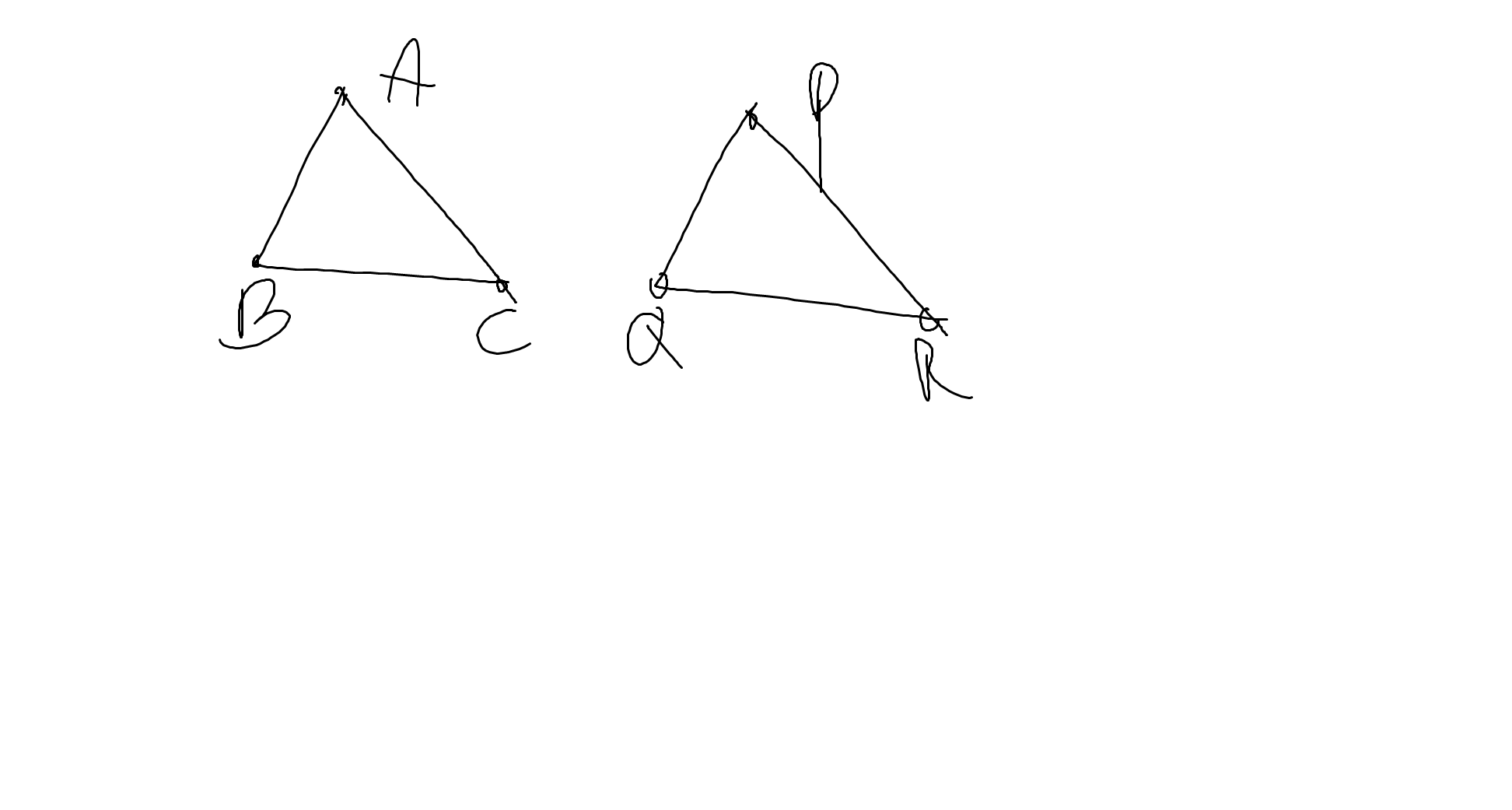
ΔABC=ΔPQR
=>\(\widehat{B}=\widehat{Q}\)
=>\(\widehat{B}=55^0\)
\(3\cdot\widehat{A}=2\cdot\widehat{C}\)
=>\(\widehat{A}=\dfrac{2}{3}\cdot\widehat{C}\)
Xét ΔABC có \(\widehat{A}+\widehat{C}+\widehat{B}=180^0\)
=>\(\dfrac{2}{3}\cdot\widehat{C}+\widehat{C}=180^0-55^0=125^0\)
=>\(\dfrac{5}{3}\cdot\widehat{C}=125^0\)
=>\(\widehat{C}=125^0:\dfrac{5}{3}=75^0\)
\(\widehat{A}=\dfrac{2}{3}\cdot75^0=50^0\)
ΔABC=ΔPQR
=>\(\widehat{P}=\widehat{A}=50^0;\widehat{R}=\widehat{C}=75^0\)
Bài 6:
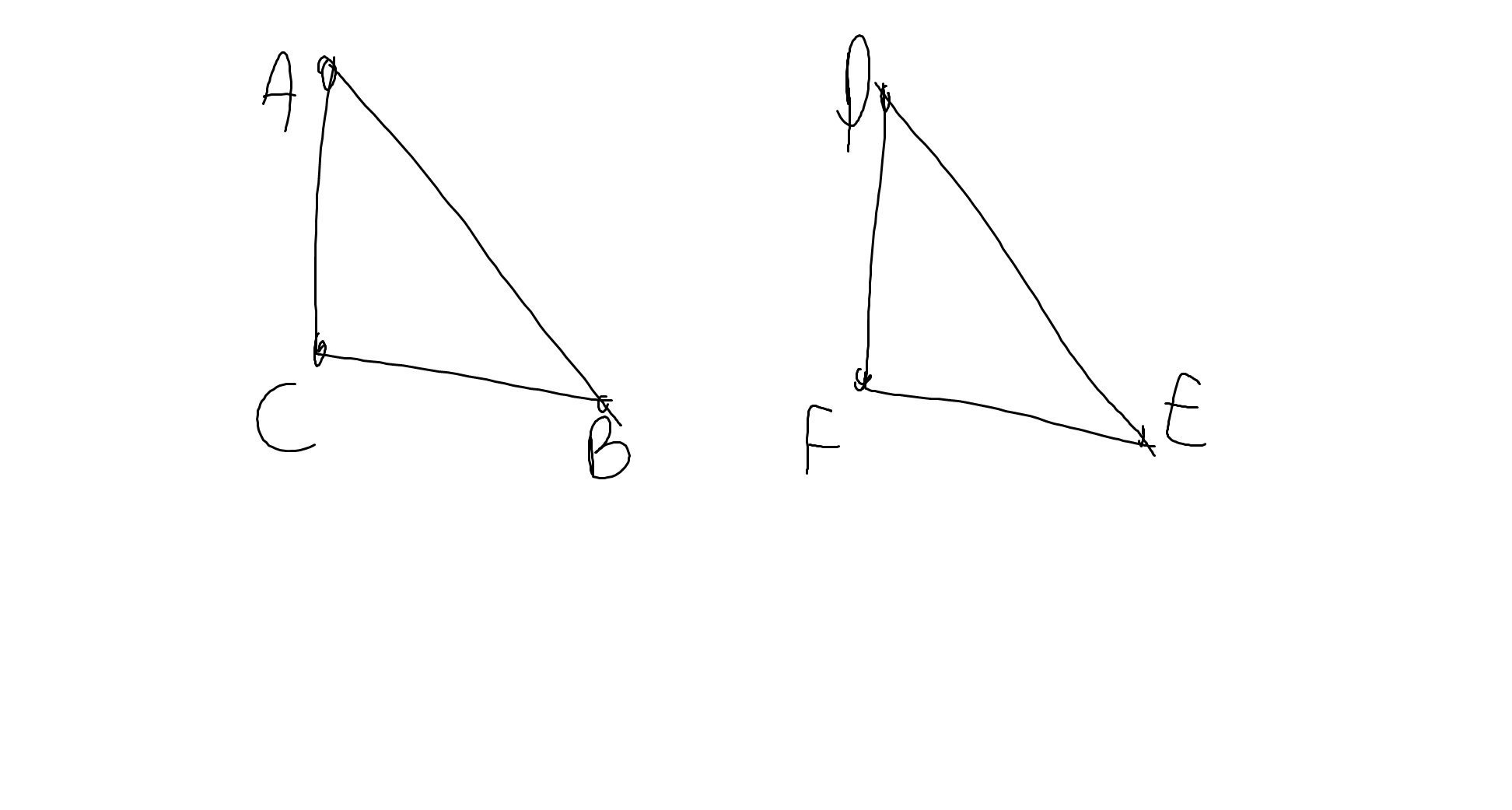
Xét ΔDEF có \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
mà \(\widehat{D}:\widehat{E}:\widehat{F}=2:3:5\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{D}}{2}=\dfrac{\widehat{E}}{3}=\dfrac{\widehat{F}}{5}=\dfrac{\widehat{D}+\widehat{E}+\widehat{F}}{2+3+5}=\dfrac{180^0}{10}=18^0\)
=>\(\left\{{}\begin{matrix}\widehat{D}=2\cdot18^0=36^0\\\widehat{E}=3\cdot18^0=54^0\\\widehat{F}=5\cdot18^0=90^0\end{matrix}\right.\)
ΔABC=ΔDEF
=>\(\widehat{A}=\widehat{D}=36^0;\widehat{B}=\widehat{E}=54^0;\widehat{C}=\widehat{F}=90^0\)

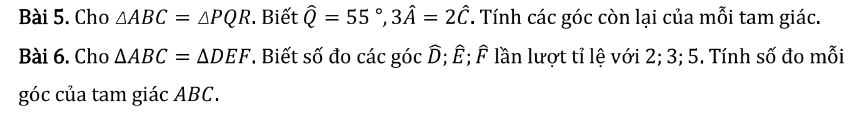 GIẢI không cần vẽ
GIẢI không cần vẽ