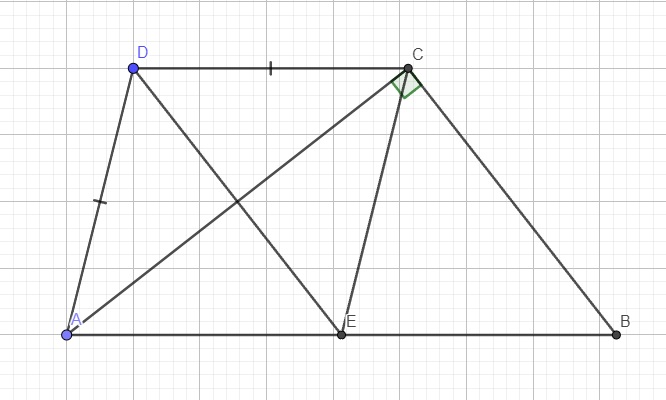
a.
Theo giả thiết ta có: \(\left\{{}\begin{matrix}AB||CD\Rightarrow AE||CD\\CE||AD\end{matrix}\right.\)
\(\Rightarrow AECD\) là hình bình hành
Lại có \(AD=CD\) (giả thiết)
\(\Rightarrow AECD\) là hình thoi (hbh có 2 cạnh kề bằng nhau)
b.
Do \(AB||CD\Rightarrow BE||CD\) (1)
Theo cmt AECD là hình thoi \(\Rightarrow AC\perp DE\) (t/c hai đường chéo hình thoi)
Theo giả thiết \(AC\perp BC\)
\(\Rightarrow DE||BC\) (2)
(1);(2) \(\Rightarrow BEDC\) là hbh (tứ giác có 2 cặp cạnh đối song song)
c.
Do BEDC là hình bình hành (cmt) \(\Rightarrow BE=CD\)
Do AECD là hình thoi (cmt câu a) \(\Rightarrow CE=CD\)
\(\Rightarrow BE=CE\)
\(\Rightarrow\Delta CEB\) cân tại E

 tuii cần gấp ạ giải gấp giúp tui với
tuii cần gấp ạ giải gấp giúp tui với 




 giúp tui với tui đang cần gấp ạ xong tui tick
giúp tui với tui đang cần gấp ạ xong tui tick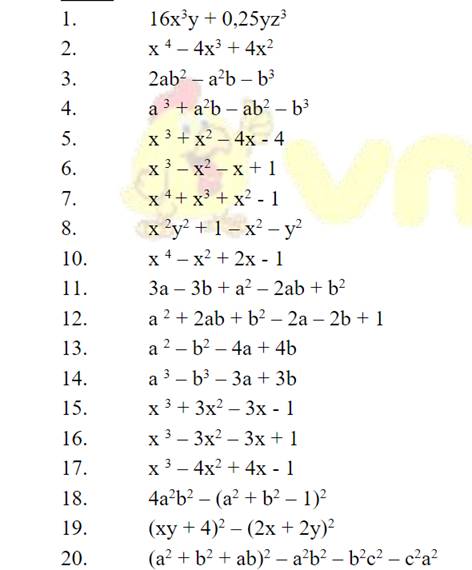
 giúp tui với ạ trước 10h nha tui đang cần gấp
giúp tui với ạ trước 10h nha tui đang cần gấp
 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
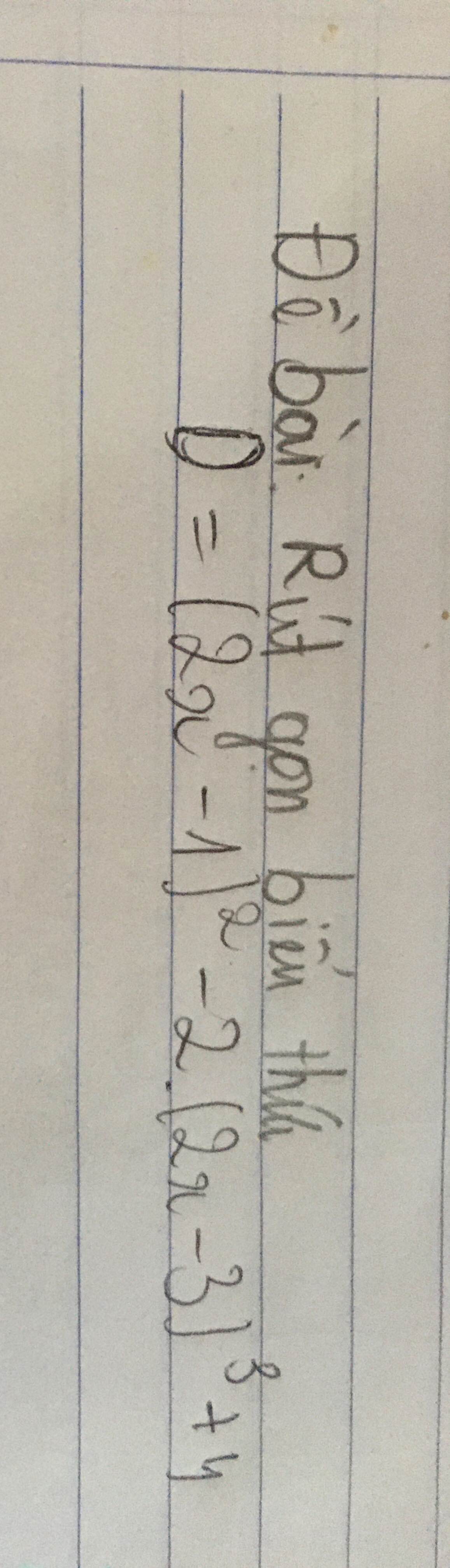

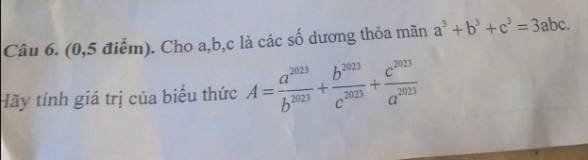

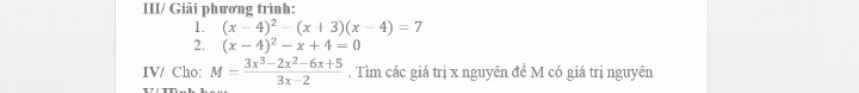

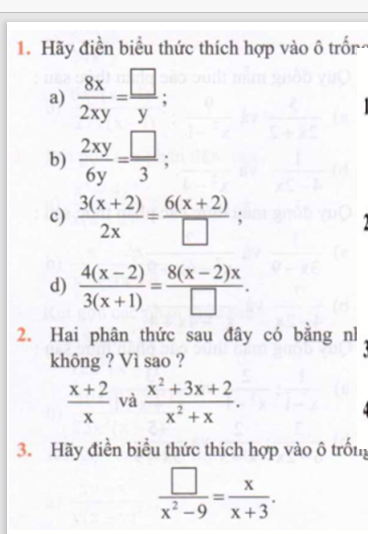 Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ

