Các câu hỏi tương tự
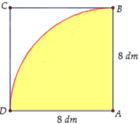
Từ miếng tôn hình vuông cạnh bằng 4dm. Người ta cắt ra hình quạt tâm O bán kính
O
A
4
dm (hình vẽ) để cuộn lại thành một chiếc phễu hình nón (khi đó OA trùng với OB). Chiều cao của chiếc phếu có số đo gần đúng (làm tròn đến 3 chữ số thập phân) là A. 3,872 dm B. 3,874 dm C. 3,871 dm D. 3,873 dm
Đọc tiếp
Từ miếng tôn hình vuông cạnh bằng 4dm. Người ta cắt ra hình quạt tâm O bán kính O A = 4 dm (hình vẽ) để cuộn lại thành một chiếc phễu hình nón (khi đó OA trùng với OB). Chiều cao của chiếc phếu có số đo gần đúng (làm tròn đến 3 chữ số thập phân) là
A. 3,872 dm
B. 3,874 dm
C. 3,871 dm
D. 3,873 dm
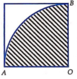
Với một miếng tôn hình tròn có bán kính bằng R9cm. Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Hình nón có thể tích lớn nhất khi độ dài cung tròn của hình quạt tạo thành hình nón bằng A.
8
π
6
c
m
B.
2
π
6
c
m
C. ...
Đọc tiếp
Với một miếng tôn hình tròn có bán kính bằng R=9cm. Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Hình nón có thể tích lớn nhất khi độ dài cung tròn của hình quạt tạo thành hình nón bằng
A. 8 π 6 c m
B. 2 π 6 c m
C. π 6 c m
D. 6 π 6 c m
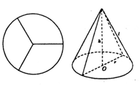
Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60cm thành ba miếng hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu? A. V
16000
2
3
lít B. V
16
π
2
3...
Đọc tiếp
Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60cm thành ba miếng hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu?
A. V= 16000 2 3 lít
B. V= 16 π 2 3 lít
C. 16000 π 2 3 lít
D. 160 π 2 3 lít
Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60cm thành ba miền hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu? A.
V
16000
2
3
l
í
t
B.
V
16...
Đọc tiếp
Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60cm thành ba miền hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu?
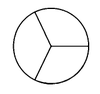
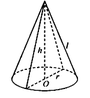
A. V = 16000 2 3 l í t
B. V = 16 2 3 l í t
C. V = 16000 2 π 3 l í t
D. V = 160 2 π 3 l í t
Cho hình nón có thể tích bằng 12
π
và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương. A. 4 B. 3. C. 6 D. 5
Đọc tiếp
Cho hình nón có thể tích bằng 12 π và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
A. 4
B. 3.
C. 6
D. 5
Từ miếng bìa hình tròn kính R 4 người ta cắt một hình quạt có bán kính với hình tròn và góc
α
270
°
. Sau đó xếp hình quạt thành mặt xung quanh của hình nón. Tính thể tích cùa khối nón. A.
4
π
B.
3
π
7
C.
9
π
7
D.
64
π
3
Đọc tiếp
Từ miếng bìa hình tròn kính R = 4 người ta cắt một hình quạt có bán kính với hình tròn và góc α = 270 ° . Sau đó xếp hình quạt thành mặt xung quanh của hình nón. Tính thể tích cùa khối nón.
A. 4 π
B. 3 π 7
C. 9 π 7
D. 64 π 3
Cho miếng tôn hình tròn tâm O bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O hông đáy (OA trùng với OB). Gọi S, S’ lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số
S
S
để thể tích khối nón lớn nhất A.
6
3
B.
1
4...
Đọc tiếp
Cho miếng tôn hình tròn tâm O bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O hông đáy (OA trùng với OB). Gọi S, S’ lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số S ' S để thể tích khối nón lớn nhất
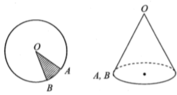
A. 6 3
B. 1 4
C. 2 3
D. 1 3
Bạn An có một tâm bìa hình tròn như hình vẽ. An muốn biến hình tròn đó thành một cái phễu hình nón. Khi đó An phải cắt bỏ hình quạt tròn OAB rồi dán hai bán kính OA và OB lại với nhau. Gọi x là góc ở tâm hình quạt tròn dùng để làm phễu. Tìm x để thể tích phễu lớn nhất. A.
π
4
B.
2
6
π
3...
Đọc tiếp
Bạn An có một tâm bìa hình tròn như hình vẽ. An muốn biến hình tròn đó thành một cái phễu hình nón. Khi đó An phải cắt bỏ hình quạt tròn OAB rồi dán hai bán kính OA và OB lại với nhau. Gọi x là góc ở tâm hình quạt tròn dùng để làm phễu. Tìm x để thể tích phễu lớn nhất.
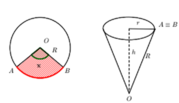
A. π 4
B. 2 6 π 3
C. π 3
D. π 2
Cho một miếng tôn hình tròn tâm O, bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O không có đáy (OA trùng với OB). Gọi S và S lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số
S
S
để thể tích của khối nón đạt giá trị lớn nhất A.
2
3...
Đọc tiếp
Cho một miếng tôn hình tròn tâm O, bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O không có đáy (OA trùng với OB). Gọi S và S ' lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số S S ' để thể tích của khối nón đạt giá trị lớn nhất
A. 2 3
B. 1 4
C. 1 3
D. 6 3