Các câu hỏi tương tự
Cho tứ diện ABCD có
A
B
C
D
a
,
A
C
B
D
b
,
A
D
B
C
c
. Khoảng cách giữa hai đường thẳng AB và CD là
Đọc tiếp
Cho tứ diện ABCD có A B = C D = a , A C = B D = b , A D = B C = c . Khoảng cách giữa hai đường thẳng AB và CD là
![]()
![]()
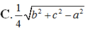
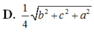
Cho tứ diện ABCD có AB AD a
2
, BC BD a và CA CD x. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a
3
3
12
. Góc giữa hai mặt phẳng (ACD) và (BCD) là: A.600 B.450 C.900 D.1200
Đọc tiếp
Cho tứ diện ABCD có AB = AD = a 2 , BC = BD = a và CA = CD = x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A.600
B.450
C.900
D.1200
Cho hình chóp S.ABCD có đáy là hình thang cân,
B
C
∥
A
D
,
A
B
B
C
C
D
a
,
A
D
2
a
. Biết rằng hình chiếu vuông góc của đỉnh S xuống đáy trùng với trung điểm H của AD. Biết rằng
S
H
a
khoảng cách giữa hai đường thẳng AD và SB bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang cân, B C ∥ A D , A B = B C = C D = a , A D = 2 a . Biết rằng hình chiếu vuông góc của đỉnh S xuống đáy trùng với trung điểm H của AD. Biết rằng S H = a khoảng cách giữa hai đường thẳng AD và SB bằng
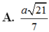
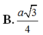
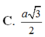
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c. Chứng minh rằng các đường vuông góc chung của các cặp cạnh đối diện đồng quy và đôi một vuông góc với nhau
Cho tứ diện đều ABCD cạnh a. Tính khoảng cách h giữa AB và CD. A. h
a
2
2
B. h
a
2
C. h
a
2
3
D. h
a
3
2
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Tính khoảng cách h giữa AB và CD.
A. h = a 2 2
B. h = a 2
C. h = a 2 3
D. h = a 3 2
Hình chóp S.ABCD đáy ABCD là hình thang vuông tại A, B; SA ^ (ABCD) với SA AB BC a, AD 2a. Tính khoảng cách h giữa AC, SD. A. h a
2
3
B. h
a
3
2
C. h
a
2
D. h
2
a
5
Đọc tiếp
Hình chóp S.ABCD đáy ABCD là hình thang vuông tại A, B; SA ^ (ABCD) với SA = AB = BC = a, AD = 2a. Tính khoảng cách h giữa AC, SD.
A. h = a 2 3
B. h = a 3 2
C. h = a 2
D. h = 2 a 5
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD 2a, AB BC SA a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD). A. h
a
3
B. h
a
6
6
C. h
a
6
3
D. h
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD = 2a, AB = BC = SA = a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).
A. h = a 3
B. h = a 6 6
C. h = a 6 3
D. h = a 3 6
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC AD 4, AB 3, BC 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD). A.
34
12
B.
12
34
C.
769
60
D.
60
769
Đọc tiếp
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 34 12
B. 12 34
C. 769 60
D. 60 769
Cho tứ diện ABCD có BCa, CDa
3
,
B
C
D
^
A
B
C
^
A
D
C
^
90
°
. Góc giữa đường thẳng AD và BC bằng 60...
Đọc tiếp
Cho tứ diện ABCD có BC=a, CD=a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa đường thẳng AD và BC bằng 60 ° . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
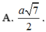
![]()
![]()



