Các câu hỏi tương tự
Cho hình lăng trụ tứ giác đều, cạnh đáy bằng a, cạnh bên bằng b. Diện tích toàn phần của hình lăng trụ là A.
S
t
p
2
a
2
+
4
a
b
. B.
S
t
p
2
a
2
+...
Đọc tiếp
Cho hình lăng trụ tứ giác đều, cạnh đáy bằng a, cạnh bên bằng b. Diện tích toàn phần của hình lăng trụ là
A. S t p = 2 a 2 + 4 a b .
B. S t p = 2 a 2 + 16 a b .
C. S t p = a 2 + 4 a b .
D. S t p = a 2 + 16 a b .
Cho hình lăng trụ tam giác đều ABC.ABC có tất cả các cạnh bằng 2. Gọi M,N,P lần lượt là trung điểm các cạnh AB,BB′ và A’C’ (tham khảo hình vẽ bên). Thể tích của khối tứ diện CMNP bằng A.
5
3
12
B.
2
3
3
C.
5
3
4
D. ...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 2. Gọi M,N,P lần lượt là trung điểm các cạnh AB,BB′ và A’C’ (tham khảo hình vẽ bên). Thể tích của khối tứ diện CMNP bằng
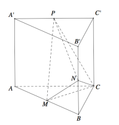
A. 5 3 12
B. 2 3 3
C. 5 3 4
D. 5 3 8
Trong các loại hình sau: Tứ diện đều; hình chóp tứ giác đều; hình lăng trụ tam giác đều; hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất. A. Tứ diện đều B. Hình chóp tứ giác đều C. Hình lăng trụ tam giác đều D. Hình hộp chữ nhật
Đọc tiếp
Trong các loại hình sau: Tứ diện đều; hình chóp tứ giác đều; hình lăng trụ tam giác đều; hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất.
A. Tứ diện đều
B. Hình chóp tứ giác đều
C. Hình lăng trụ tam giác đều
D. Hình hộp chữ nhật
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều có cạnh bằng a, cạnh bên tạo với đáy góc 300. Biết hình chiếu vuông góc của A’ trên trùng với trung điểm cạnh BC. Tính bán kính mặt cầu ngoại tiếp tứ diện A’ABC. A.
a
3
B.
a
3
2
C.
a
3
6
D.
a...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều có cạnh bằng a, cạnh bên tạo với đáy góc 300. Biết hình chiếu vuông góc của A’ trên trùng với trung điểm cạnh BC. Tính bán kính mặt cầu ngoại tiếp tứ diện A’ABC.
A. a 3
B. a 3 2
C. a 3 6
D. a 3 3
Cho hình bát diện đều ABCDEF cạnh a. Tính theo a thể tích V của khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện (xem hình vẽ) A.
V
a
3
2
.
B.
V
a
3
2
4
.
C.
V
a...
Đọc tiếp
Cho hình bát diện đều ABCDEF cạnh a. Tính theo a thể tích V của khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện (xem hình vẽ)
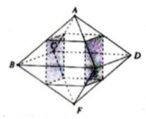
A. V = a 3 2 .
B. V = a 3 2 4 .
C. V = a 3 2 2 .
D. V = a 3 2 8 .
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a. A.
5
π
a
2
3
B.
7
π
a
2
3
C.
3
π
a
2
D. ...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
A. 5 π a 2 3
B. 7 π a 2 3
C. 3 π a 2
D. 11 π a 2 3
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a. A.
S
17
πa
2
13
B.
S
7
πa
2
3
C.
S
17
πa
2...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
A. S = 17 πa 2 13
B. S = 7 πa 2 3
C. S = 17 πa 2
D. S = 7 π a 2
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a. A.
5
π
a
2
3
B.
7
π
a
2
3
C.
3
π
a
2
D. ...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A¢B¢C¢ có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
A. 5 π a 2 3
B. 7 π a 2 3
C. 3 π a 2
D. 11 π a 2 3
Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều (như hình vẽ). Gọi
V
1
;
V
2
lần lượt là thể tích của lăng trụ tứ giác đều và lăng trụ tam giác đều. So sánh
V...
Đọc tiếp
Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều (như hình vẽ). Gọi V 1 ; V 2 lần lượt là thể tích của lăng trụ tứ giác đều và lăng trụ tam giác đều. So sánh V 1 và V 2
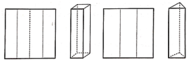
A. V 1 > V 2
B. V 1 = V 2
C. V 1 < V 2
D. Không so sánh được



