Các câu hỏi tương tự
Cho hình nón (N) có bán kính r 20(cm), chiều cao h 60(cm) và mọt hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất? A. V3000
π
(
cm
3
)
. B. V
32000
9...
Đọc tiếp
Cho hình nón (N) có bán kính r = 20(cm), chiều cao h = 60(cm) và mọt hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
A. V=3000 π ( cm 3 ) .
B. V= 32000 9 π ( cm 3 ) .
C. V=3600 π ( cm 3 ) .
D. V=4000 π ( cm 3 ) .
Cho hình nón có đường cao h 3 và bán kính đáy R 4. Diện tích xung quanh
S
x
q
của hình nón là A.
S
x
q
12
π
.
B.
S
x
q
24
π
.
C.
S...
Đọc tiếp
Cho hình nón có đường cao h = 3 và bán kính đáy R = 4. Diện tích xung quanh S x q của hình nón là
A. S x q = 12 π .
B. S x q = 24 π .
C. S x q = 20 π .
D. S x q = 15 π .
Cho hình nón có bán kính đáy r1, chiều cao
h
3
Tính diện tích xung quanh
S
x
q
của hình nón đó A.
S
x
q
2
3
π
B.
S
x
q
3
π
C. ...
Đọc tiếp
Cho hình nón có bán kính đáy r=1, chiều cao h = 3 Tính diện tích xung quanh S x q của hình nón đó
A. S x q = 2 3 π
B. S x q = 3 π
C. S x q = 4 π
D. S x q = 2 π
Cho hình nón có bán kính đáy r 1 chiều cao
h
3
Tính diện tích xung quanh
S
x
q
của hình nón đó. A.
S
x
q...
Đọc tiếp
Cho hình nón có bán kính đáy r = 1 chiều cao h = 3 Tính diện tích xung quanh S x q của hình nón đó.
A. S x q = 2 3 π .
B. S x q = 3 π .
C. S x q = 4 π .
D. S x q = 2 π .
Cho hình nón bán kính
r
12
nội tiếp hình cầu bán kính
r
13
(như hình vẽ). Tính diện tích xung quanh
S
x
q
của hình nón A.
S
x
q
36
13
π
.
B.
S
x...
Đọc tiếp
Cho hình nón bán kính r = 12 nội tiếp hình cầu bán kính r = 13 (như hình vẽ).
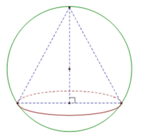
Tính diện tích xung quanh S x q của hình nón
A. S x q = 36 13 π .
B. S x q = 72 5 π .
C. S x q = 36 5 π .
D. S x q = 72 13 π .
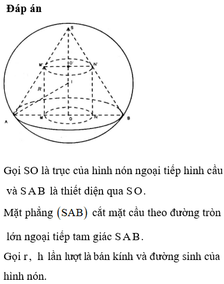
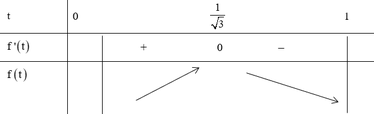
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (C). Gọi h là chiều cao của hình nón. Tìm h để thể tích của khối nón là lớn nhất. A.
4
r
3
B.
r
3
C.
r
6
D.
7
r
6
Đọc tiếp
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (C). Gọi h là chiều cao của hình nón. Tìm h để thể tích của khối nón là lớn nhất.
A. 4 r 3
B. r 3
C. r 6
D. 7 r 6
Cho hình nón (N) có chiều cao h = 4, bán kính đường tròn đáy r = 3. Diện tích xung quanh của hình nón (N) bằng:
A. 12 π
B. 20 π
C. 15 π
D. 30 π
Cho hình cầu (S) tâm I, bán kính R không đổi. Một hình trụ có chiều cao h và bán kính r thay đổi nội tiếp hình cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất A.
h
R
2
B. h R C.
h
R
2
D.
h
R
2
2
Đọc tiếp
Cho hình cầu (S) tâm I, bán kính R không đổi. Một hình trụ có chiều cao h và bán kính r thay đổi nội tiếp hình cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất
A. h = R 2
B. h = R
C. h = R 2
D. h = R 2 2
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất. A.
h
R
2
B.
h
R
C.
h
R
2
D.
h
R
2...
Đọc tiếp
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
A. h = R 2
B. h = R
C. h = R 2
D. h = R 2 2