Các câu hỏi tương tự
Cho hình nón có thể tích bằng 12
π
và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương. A. 4 B. 3. C. 6 D. 5
Đọc tiếp
Cho hình nón có thể tích bằng 12 π và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
A. 4
B. 3.
C. 6
D. 5
Cho hình tròn tâm S, bán kính R 2 . Cắt đi
1
4
hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó. A.
21
π
4
B.
3
+
4
3
π
C.
3
+
2...
Đọc tiếp
Cho hình tròn tâm S, bán kính R = 2 . Cắt đi 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó.
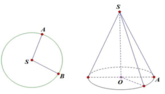
A. 21 π 4
B. 3 + 4 3 π
C. 3 + 2 3 π
D. 3 π
Cho hình nón có bán kính đáy là
r
3
và độ dài đường sinh l 4 .Tính diện tích xung quanh S của hình nón đã cho A.
S
8
3
π
B.
S
24
π
C.
S
16
3
π
D.
S
4
3
π
Đọc tiếp
Cho hình nón có bán kính đáy là r = 3 và độ dài đường sinh l = 4 .Tính diện tích xung quanh S của hình nón đã cho
A. S = 8 3 π
B. S = 24 π
C. S = 16 3 π
D. S = 4 3 π
Cho hình nón có bán kính đáy là
r
2
và độ dài đường sinh l 4. Tính diện tích xung quanh S của hình nón đã cho A.
S
16
π
B.
S
8
2
π
C.
S
16
2
π
D.
S
4
2
π
Đọc tiếp
Cho hình nón có bán kính đáy là r = 2 và độ dài đường sinh l = 4. Tính diện tích xung quanh S của hình nón đã cho
A. S = 16 π
B. S = 8 2 π
C. S = 16 2 π
D. S = 4 2 π
Cho hình nón đỉnh S có bán kính
R
a
2
góc ở đỉnh bằng 60 độ Diện tích xung quanh của hình nón bằng A.
π
a
2
B.
4
π
a
2
C.
6
π
a
2
D.
2
π
a
2
Đọc tiếp
Cho hình nón đỉnh S có bán kính R = a 2 góc ở đỉnh bằng 60 độ Diện tích xung quanh của hình nón bằng
A. π a 2
B. 4 π a 2
C. 6 π a 2
D. 2 π a 2
Cho hình nón đỉnh S có bán kính đáy
R
a
2
,
góc ở đình bằng
60
0
.
Diện tích xung quanh của hình nón bằng A.
π
a
2
.
B.
4
π
a
2
.
C.
6
π
a
2
.
D.
2
π...
Đọc tiếp
Cho hình nón đỉnh S có bán kính đáy R = a 2 , góc ở đình bằng 60 0 . Diện tích xung quanh của hình nón bằng
A. π a 2 .
B. 4 π a 2 .
C. 6 π a 2 .
D. 2 π a 2 .
Cho hình nón đỉnh S có bán kính đáy
R
a
2
, góc ở đỉnh bằng
60
0
. Diện tích xung quanh của hình nón bằng A.
π
a
2
B.
4
π
a
2
C.
6
π
a
2
D.
2
π...
Đọc tiếp
Cho hình nón đỉnh S có bán kính đáy R = a 2 , góc ở đỉnh bằng 60 0 . Diện tích xung quanh của hình nón bằng
A. π a 2
B. 4 π a 2
C. 6 π a 2
D. 2 π a 2
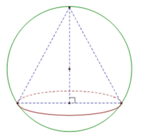
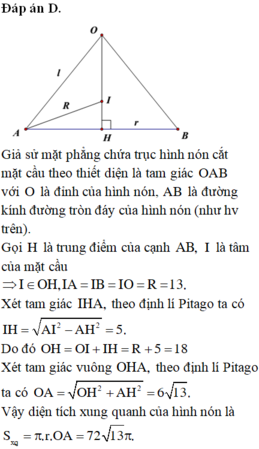
Cho khối cầu tâm I, bán kính R. Gọi S là điểm cố định thỏa mãn IS 2R. Từ S, kẻ tiếp tuyến SM với khối cầu (với M là tiếp điểm). Tập hợp các đoạn thẳng SM khi M thay đổi là mặt xung quanh của hình nón đỉnh S. Tính diện tích xung quanh
S
x
q
của hình nón đó, biết rằng tập hợp các điểm M là đường tròn có chu vi
2
π
3
. A.
S
x...
Đọc tiếp
Cho khối cầu tâm I, bán kính R. Gọi S là điểm cố định thỏa mãn IS = 2R. Từ S, kẻ tiếp tuyến SM với khối cầu (với M là tiếp điểm). Tập hợp các đoạn thẳng SM khi M thay đổi là mặt xung quanh của hình nón đỉnh S. Tính diện tích xung quanh S x q của hình nón đó, biết rằng tập hợp các điểm M là đường tròn có chu vi 2 π 3 .
A. S x q = 6 π
B. S x q = 9 π
C. S x q = 3 π
D. S x q = 12 π
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng
60
°
. Tính tỉ số thể tích của hình trụ (N) và hình nón (T). A.
V
T
V
N
2
6
B. ...
Đọc tiếp
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (N) và hình nón (T).
A. V T V N = 2 6
B. V T V N = 2 3
C. V T V N = 3 2
D. Đáp án khác