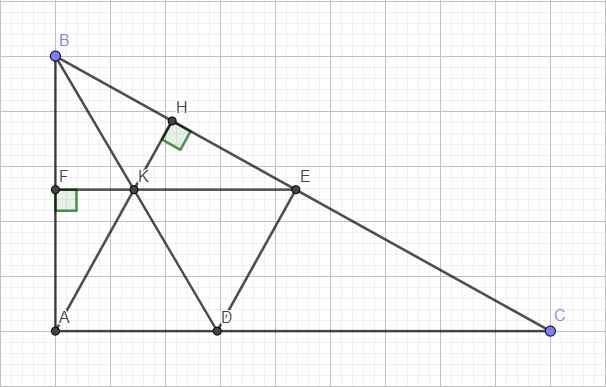
Trong một mặt phẳng toạ độ xOy cho tam giác AC vuông tại A có đường cao AH: x- 3y-16=0 cắt đường phân giác BD tại K( \(D\in AC\)) , đường thẳng đi qua K song song với AC và cắt cạnh huyền BC tại E ( 3;-7), biết điểm D thuộc đường thẳng\(\Delta:x-y-12=0\) và xA>3. Viết phương trình các cạnh của tam giác ABC
Hướng dẫn, hơi dài nên làm biếng giải chi tiết:
Kéo dài KE cắt AB tại F
BK là phân giác góc B nên hai tam giác vuông BKH và BKF bằng nhau (ch-gn)
\(\Rightarrow\widehat{BKF}=\widehat{BKE}\) \(\Rightarrow\widehat{BKA}=\widehat{BKE}\)
\(\Rightarrow\Delta BKA=\Delta BKE\left(g.c.g\right)\)
\(\Rightarrow AK=EK\)
Lại có \(\widehat{BKF}=\widehat{BDA}\) (đồng vị) \(\Rightarrow\widehat{BDA}=\widehat{BKH}=\widehat{AKD}\)
\(\Rightarrow\Delta AKD\) cân tại A hay \(AK=AD\)
\(\Rightarrow AD=EK\Rightarrow ADEK\) là hình bình hành hay DE song song AK (hay AH)
BC vuông góc AH nên nhận (3;1) là 1 vtpt và đi qua E(3;-7) \(\Rightarrow\) pt BC
ED đi qua E(3;-7) và song song AH nên nhận (1;-3) là 1 vtpt \(\Rightarrow\) pt DE
\(\Rightarrow\) Tọa độ D (giao của DE và \(\Delta\))
ADEK là hbh (theo cmt) và có 2 cạnh kề AK=AD nên ADEK là hình thoi
\(\Rightarrow AD=DE\)
Biết tọa độ D, E \(\Rightarrow\) độ dài DE
A thuộc AH nên tọa độ A có dạng: \(A\left(3a+16;a\right)\Rightarrow\overrightarrow{DA}=...\Rightarrow\left|\overrightarrow{DA}\right|=DE\)
\(\Rightarrow a\Rightarrow\) tọa độ A
\(\Rightarrow\) Phương trình AC (qua A và D)
\(\Rightarrow\) Phương trình AB (qua A và vuông góc AC)