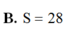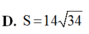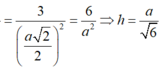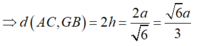Các câu hỏi tương tự
Trong không gian cho ABCD là hình chữ nhật,
A
B
2
,
A
D
1
. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết
d
A
B
,
d...
Đọc tiếp
Trong không gian cho ABCD là hình chữ nhật, A B = 2 , A D = 1 . Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d A B , d < d C D , d . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
![]()
![]()
![]()
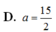
Cho khối lăng trụ ABC.ABC, hình chiếu của điểm A lên mặt phẳng (ABC) là trung điểm M của cạnh BC và AMa
3
, hình chiếu của điểm A lên mặt phẳng (BCCB) là H sao cho MH song song với BB và AHa, khoảng cách giữa hai đường thẳng BB , CC bằng 2a . Thể tích khối lăng trụ đã cho là A.
3
2
a
3
B.
2...
Đọc tiếp
Cho khối lăng trụ ABC.A'B'C', hình chiếu của điểm A lên mặt phẳng (A'B'C') là trung điểm M của cạnh B'C' và A'M=a 3 , hình chiếu của điểm A lên mặt phẳng (BCC'B') là H sao cho MH song song với BB' và AH=a, khoảng cách giữa hai đường thẳng BB' , CC' bằng 2a . Thể tích khối lăng trụ đã cho là
A. 3 2 a 3
B. 2 a 3
C. 2 2 a 3 3
D. 3 2 a 3 2
Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto làm vectơ chỉ phương và song song với mặt phẳng (P): 2x+y+z0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng: A. 15 B. 13 C. 16 D. 14
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto làm vectơ chỉ phương và song song với mặt phẳng (P): 2x+y+z=0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng:
A. 15
B. 13
C. 16
D. 14
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0; 4), D(4; 0; 6) Hãy viết phương trình mặt phẳng (α) đi qua cạnh AB và song song với cạnh CD.
Trong không gian Oxyz, cho mặt phẳng (P) đi qua hai điểm A(1;2;3), B(3;-1;1) và song song với đường thẳng d:
x
-
1
2
y
+
2
-
1
z
-
3
1
. Khoảng cách từ...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P) đi qua hai điểm A(1;2;3), B(3;-1;1) và song song với đường thẳng d: x - 1 2 = y + 2 - 1 = z - 3 1 . Khoảng cách từ gốc tọa độ đến mặt phẳng bằng
A. 37 101
B. 5 77
C. 37 101
D. 5 77 77
Trong không gian Oxyz, cho mặt phẳng (α): 2x+y-2z-20, đường thẳng
d
:
x
+
1
1
y
+
2
2
z
+
3
2
và điểm
A
(
1
2
;
1
;
1...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (α): 2x+y-2z-2=0, đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A ( 1 2 ; 1 ; 1 ) . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
A. 7/2
B. 21 / 2
C. 7/3
D. 3/2
Cho hình trụ có hai đáy là hai hình tròn (O) và (O'). Một mặt phẳng song song với trục và cách trục của hình trụ một khoảng bằng \(\dfrac{10a}{3}\), cắt hình trụ theo thiết diện một hình vuông ABCD, A \(\in\) (O'). Biết góc giữa OA và mặt phẳng (ABCD) bằng \(30^o\). Tính thể tích khối trụ đã cho bằng
Trong không gian với hệ tọa độ Oxyz, cho (P): x - 2y + 2z -5 0, A (-3; 0; 1), b (1; -1; 3). Viết phương trình đường thẳng d đi qua A, song song với (P) sao cho khoảng cách từ B đến d là lớn nhất.
A
.
x
+
3
1
y
-
1
z
-
1
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho (P): x - 2y + 2z -5 = 0, A (-3; 0; 1), b (1; -1; 3). Viết phương trình đường thẳng d đi qua A, song song với (P) sao cho khoảng cách từ B đến d là lớn nhất.
A . x + 3 1 = y - 1 = z - 1 2
B . x + 3 3 = y - 2 = z - 1 2
C . x - 1 1 = y - 2 = z - 1 2
D . x + 3 2 = y - 6 = z - 1 - 7
Một hình trụ có bán kính đáy bằng 5 và khoảng cách giữa hai đáy bằng 7. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 3. Tính diện tích S của thiết diện được tạo thành.
Đọc tiếp
Một hình trụ có bán kính đáy bằng 5 và khoảng cách giữa hai đáy bằng 7. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 3. Tính diện tích S của thiết diện được tạo thành.