Gọi (P) là mặt phẳng đi qua cạnh AB và song song với cạnh CD. Mặt phẳng (P) có vecto pháp tuyến n → vuông góc với hai vecto A B → = - 4 ; 5 ; - 1 v à C D → - 1 ; 0 ; 2
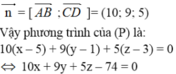
Gọi (P) là mặt phẳng đi qua cạnh AB và song song với cạnh CD. Mặt phẳng (P) có vecto pháp tuyến n → vuông góc với hai vecto A B → = - 4 ; 5 ; - 1 v à C D → - 1 ; 0 ; 2
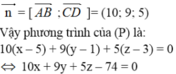
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0 ; 4), D(4; 0 ; 6). Hãy viết phương trình mặt phẳng ( α ) đi qua điểm D và song song với mặt phẳng (ABC).
Cho tứ diện có các đỉnh là A(5;1;3), B(1;6;2), C(5;0;4), D(4;0;6). Tìm phương trình mặt phẳng (P) đi qua cạnh AB và song song với cạnh CD.
![]()
![]()
![]()
![]()
Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0) Viết phương trình mặt phẳng (α) chứa AB và song song với CD.
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0; 4), D(4; 0; 6) Hãy viết phương trình của các mặt phẳng (ACD) và (BCD)
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0 ; 4), D(4; 0 ; 6). Hãy viết phương trình mặt phẳng (ABC).
Hãy viết phương trình mặt phẳng (α) đi qua điểm M(2; -1; 2) và song song với mặt phẳng (β) : 2x – y + 3z + 4 = 0
Cho điểm M(3;-1;-2) và mặt phẳng α : 3x-y+z+4=0. Phương trình nào sau đây là phương trình mặt phẳng đi qua M và song song với α
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho điểm M (3;-1;-2) và mặt phẳng ( α ): 3x-y+2z+4=0. Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với ( α )?
A. 3x+y-2z-14=0
B. 3x-y+2z+6=0
C. 3x-y+2z-6=0
D. 3x-y-2z+6=0
Viết phương trình mặt phẳng ( α ) trong các trường hợp sau: ( α ) đi qua điểm A(1; 0; 0) và song song với giá của hai vecto u → = (0; 1; 1), v → = (−1; 0; 2)